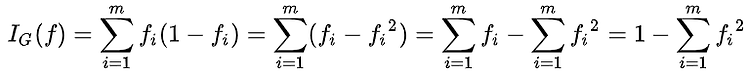

의사결정나무는 무엇이며 , R에서 어떻게 구현할 수 있으며 , 그 의미는 무엇인지 알아 볼 것이다.
의사결정나무(decision tree) 또는 나무 모형(tree model)은 의사결정 규칙을 나무 구조로 나타내어 전체 자료를 몇 개의 소집단으로 분류(classification) 하거나 예측 (prediction)을 수행하는 분석방법이다.
상위 노드로부터 하위노드로 트리구조를 형성하는 매 단계마다 분류변수와 분류 기준값의 선택이 중요하다. 상위노드에서의 (분류변수 , 분류 기준값)은 이 기준에 의해 분기되는 하위노드에서 노드 (집단) 내에서는 동질성이 , 노드(집단)간에는 이질성이 가장 커지도록 선택된다.
나무 모형의 크기는 과대적합(또는 과소적합) 되지 않도록 합리적 기준에 의해 적당히 조절되어야 한다.
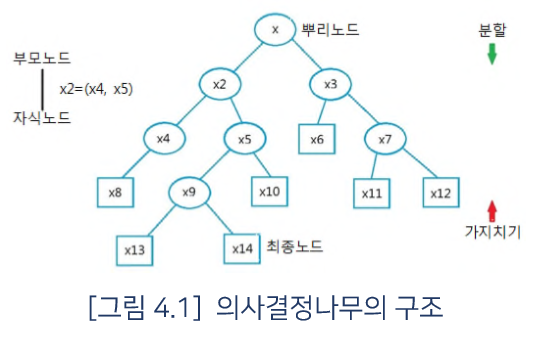
의사결정나무의 구조는 다음 그림과 같다.
이 그림에서 맨 위의 마디를 뿌리노드(root node)라 하며 , 이는 분류(또는 예측) 대상이 되는 모든 자료집단을 포함한다.
상위마디를 부모마디(parent node)라 하고 , 하위 마디를 자식마디(child node)라 하며, 더 이상 분기되지 않는 마디를 최종노드(terminal node)라고 부른다.
가지분할(split)은 나무의 가지를 생성하는 과정을 , 가지치기(pruning)는 생성된 가지를 잘라내어 모형을 단순화하는 과정을 말한다.
의사결정나무는 목표변수가 이산형인 경우의 분류나무(classification tree)와 목표변수가 연속형인 경우의 회귀나무(regression tree)로 구분된다.
목표변수가 이산형인 분류나무의 경우 상위노드에서 가지분할을 수행할 때 , 분류(기준)변수와 분류 기준값의 선택 방법으로 카이제곱 통계랑(Chi-square statistic)의 p-값 , 지니 지수 (Gini index) , 엔트로피 지수 (entropy index) 등이 사용된다.
선택된 기준에 의해 분할이 일어날 때 , 카이제곱통계량의 p-값은 그 값이 작을수록 자식노드 간의 이질성이 큼을 나타내며 , 자식노드에서의 지니 지수나 엔트로피 지수는 그 값이 클수록 자식노드 내의 이질성이 큼을 의미한다 . 따라서 이 값들이 가장 작아지는 방향으로 가지분할을 수행하게 된다.
쉽게 말해서 높은 이질성이란 것은 낮은 순수도를 의미하며 , 낮은 이질성이란 것은 높은 순수도를 의미하는 것이다 .
불확실성 측도 ( uncertainty measure ) 인 지니 지수와 엔트로피 지수에 대한 정의는 다음과 같다 . 두 지수의 값의 범위는 다르나 , 해석은 그 크기에 따라 유사하다 .
지니 지수 :
엔트로피 지수 :
위 식에서 c는 목표변수의 범주의 수이며 , 각 지수의 범위는 c=2인 경우에 해당한다 .
목표변수가 연속형인 회귀나무의 경우에는 분류변수와 분류 기준값의 선택방법으로 F-통계량의 F-값 , 분산의 감소량 등이 사용된다.
F-통계량은 일원배치법에서의 검정통계량으로 그 값이 클수록 오차의 변동에 비해 처리(treatment)의 변동이 크다는 것을 의미하며 , 이는 자식노드(처리들) 간이 이질적임을 의미하므로 , 이 값이 커지는 (p-값은 작아지는) 방향으로 가지분하을 수행(자식노드를 생성)하게 된다 .
분산의 감소량(variance reduction)도 이 값이 최대화 되는 방향으로 가지분할을 수행하게 된다.
의사결정나무의 분석과정은 다음과 같다.
1. 목표변수와 관계가 있는 설명변수들의 선택
2. 분석목적과 자료의 구조에 따라 적절한 분리기준과 정지규칙을 정하여 의사결정 나무의 생성
3. 부적절한 나뭇가지는 제거 : 가지치기
4. 이익(gain),위험(risk),비용(cost) 등을 고려하여 모형평가
5. 분류(classification) 및 예측(prediction) 수행
의사결정나무의 주요 알고리즘은 다음과 같다 .
이제 예제를 통해서 의사결정나무 분석을 어떻게 하는지 알아볼 것이다 .
Rstudio를 사용할 것이며 , rpart의 rpart()함수를 이용할 것이다.
Rpart는 recursive partitioning and regression tree의 약어이다.
그 전에 iris는 어떤 데이터 인지 맛본다 .
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
7 4.6 3.4 1.4 0.3 setosa
8 5.0 3.4 1.5 0.2 setosa
9 4.4 2.9 1.4 0.2 setosa
10 4.9 3.1 1.5 0.1 setosa
위 처럼 Length , Width 의 데이터를 포함하며 150개의 setosa가 있다 .
코드를 보면서 확인해 본다 .
c <- rpart(Species ~., data = iris)
c의 결과값
n= 150 node), split, n, loss, yval, (yprob) * denotes terminal node 1) root 150 100 setosa (0.33333333 0.33333333 0.33333333) 2) Petal.Length< 2.45 50 0 setosa (1.00000000 0.00000000 0.00000000) * 3) Petal.Length>=2.45 100 50 versicolor (0.00000000 0.50000000 0.50000000) 6) Petal.Width< 1.75 54 5 versicolor (0.00000000 0.90740741 0.09259259) * 7) Petal.Width>=1.75 46 1 virginica (0.00000000 0.02173913 0.97826087) *
Rpart를 하게 되면 , 노드의 개수와 각 노드에 포함되어진 길이 데이터들을 특정 조건에 따라 나눈뒤 몇 개가 이에 해당하는 지 수치화해서 나타내 준다 .
나눈 c에 대해서 이제 시각화를 해볼 것이다 .
plot(c, compress = T, margin=0.3)
è plot으로써 틀을 잡아준다.
text(c, cex=1.5)
è plot에 나타내어질 데이터를 표시해 준다 .
이제 predict() 함수를 이용하여 새로운 자료에 대해 예측을 수행해 볼 것이다.
여기서는 편의상 모형구축에 사용된 자료를 재대입한 결과를 제시할 것이다 .
head(predict(c, newdata=iris, type="class"))
1 2 3 4 5 6 setosa setosa setosa setosa setosa setosa Levels: setosa versicolor virginica
tail(predict(c, newdata=iris, type="class"))
145 146 147 148 149 150 virginica virginica virginica virginica virginica virginica Levels: setosa versicolor virginica
R 패키지 rpart.plot을 이용하여 적합된 의사결정나무 모형을 여러 가지 방식으로 시각화 할 수 있다.
install.packages("rpart.plot")
library(rpart.plot)
prp(c, type=4, extra=2)
최종 노드를 해석해 보면 다음과 같다 .
두 조건 (Petal.Length >=2.5 와 Petal.Width < 1.8) 을 만족하는 노드에서 49/54는 이 노드에 속하는 해당 개체가 54개이며 , 이 가운데 versicolor가 49임을 의미한다 .
따라서 이 노드에 해당되는 새로운 자료는 versicolor로 분류된다 .
rpart() 수행 결과는 다음의 정보를 제공한다.
ls(c)
[1] "call" "control" "cptable" [4] "frame" "functions" "method" [7] "numresp" "ordered" "parms" [10] "splits" "terms" "variable.importance"[13] "where" "y"
여기서 $cptable은 트리의 크기에 따른 비용-복잡도 모수 (cost-complexity parameter) 를 제공하며 , 교차타당성오차 (cross-validation error ) 를 함께 제공한다 .
이 값들은 prune() 또는 rpart.control()함수에서 가지치기(pruning)와 트리의 최대 크기(maximum size)를 조절하기 위한 옵션으로 사용된다.
다음은 교차타당성오차를 최소로 하는 트리를 형성하는 과정이다.
여기서는 위의 rpart()를 수행한 결과와 동일한 결과를 얻게 되어 그 결과는 생략한다.
c$cptable
CP nsplit rel error xerror xstd1 0.50 0 1.00 1.12 0.053266622 0.44 1 0.50 0.68 0.060969943 0.01 2 0.06 0.11 0.03192700
opt <- which.min(c$cptable[,"xerror"])
cp <- c$cptable[opt,"CP"]
prune.c <- prune(c, cp = cp)
plot(prune.c)
text(prune.c, use.n = T)
R 패키지 rpart의 plotcp() 함수를 이용하면 cp값을 그림으로 나타낼 수 있다 .
plotcp(c)
대충 감이 오는가…
약간 이렇게 쓰면 되겠다 정도로만 이해하면 좋을 것 같다.
이제 패키지 party 의 ctree() 함수를 이용하여 의사결정나무모형을 적합할 것이다.
Ctree는 conditional inference tree의 약어이다.
밑에 분석에 사용된 자료는 146명의 전립선 암 환자의 자료 ( stagec ) 이다 .
7개의 예측변수를 이용하여 범주형의 반응변수 (ploidy)를 예측 ( 또는 분류 ) 할 것이다 .
코드를 통해서 확인해 본다 .
install.packages("party")
library(party)
data("stagec")
str(stagec)
'data.frame': 146 obs. of 8 variables: $ pgtime : num 6.1 9.4 5.2 3.2 1.9 4.8 5.8 7.3 3.7 15.9 ... $ pgstat : int 0 0 1 1 1 0 0 0 1 0 ... $ age : int 64 62 59 62 64 69 75 71 73 64 ... $ eet : int 2 1 2 2 2 1 2 2 2 2 ... $ g2 : num 10.26 NA 9.99 3.57 22.56 ... $ grade : int 2 3 3 2 4 3 2 3 3 3 ... $ gleason: int 4 8 7 4 8 7 NA 7 6 7 ... $ ploidy : Factor w/ 3 levels "diploid","tetraploid",..: 1 3 1 1 2 1 2 3 1 2 ..
Stagec의 변수들과 자료형들을 확인해 볼 수 있다 .
이제 subset을 사용해서 불필요한 데이터를 제거할 것이다 .
stagec1 <- subset(stagec, !is.na(g2))
stagec2 <- subset(stagec1, !is.na(gleason))
stagec3 <- subset(stagec2, !is.na(eet))
str(stagec3)
'data.frame': 134 obs. of 8 variables: $ pgtime : num 6.1 5.2 3.2 1.9 4.8 3.7 15.9 6.3 2.9 1.5 ... $ pgstat : int 0 1 1 1 0 1 0 0 1 1 ... $ age : int 64 59 62 64 69 73 64 65 58 70 ... $ eet : int 2 2 2 2 1 2 2 2 2 2 ... $ g2 : num 10.26 9.99 3.57 22.56 6.14 ... $ grade : int 2 3 2 4 3 3 3 3 4 3 ... $ gleason: int 4 7 4 8 7 6 7 7 8 8 ... $ ploidy : Factor w/ 3 levels "diploid","tetraploid",..: 1 1 1 2 1 1 2 2 2 1 ..
제거 하고 남은 데이터를 보면 134개의 데이터가 남은 것을 확인할 수 있다.
모형구축을 위한 훈련용 자료 (training data) 와 모형의 성능을 검증하기 위한 검증용 자료 (test data) 를 70% 와 30% 로 구성한다 .
set.seed(1234)
ind <- sample(2, nrow(stagec3), replace=TRUE, prob = c(0.7,0.3))
[1] 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 2 1 2 2 1 1 1 1 1 1 2 [37] 1 1 2 2 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 2 1 2 2 1 1 1 1 2 1 1 1 1 1 2 [73] 1 2 1 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1[109] 1 1 2 1 2 1 1 2 2 1 1 2 2 2 2 2 1 1 1 1 1 1 2 1 1 1
모형을 만들기 전에 stagec 자료를 복원 추출 방법을 이용하여 두 개의 부분집합 training ( 70% ) 와 test ( 30% ) 로 만들고 결과의 재현성을 위해 random seed 를 고정하였다 .
trainData <- stagec3[ind==1,]
testData <- stagec3[ind==2,]
훈련용 자료 ( n = 20 ) 에 대해 ctree()를 적용한 결과는 다음과 같다 .
tree <- ctree(ploidy ~., data=trainData)
tree
plot(tree)
최종노드의 막대그래프 (barplot) 는 반응변수(ploidy)의 각 범주별 비율을 나타낸다.
Predict() 함수를 통해 검증용 자료에 대해 적합모형을 적용하면 다음과 같다.
testPred = predict(tree, newdata=testData)
table(testPred, testData$ploidy)
testPred diploid tetraploid aneuploid diploid 17 0 1 tetraploid 0 13 1 aneuploid 0 0 0
ctree() 함수를 이용하여 반응변수가 연속형인 경우 의사결정나무 (회귀나무) 를 통한 예측을 수행한다 .
airquality 자료에 대해 의사결정나무모형을 적합할 것이다. 먼저 반응변수 Ozone이 결측인 자료를 제외한 후 ctree() 함수를 적용한다 .
코드를 보면서 확인해 본다 .
airq <- subset(airquality, !is.na(Ozone))
head(airq)
Ozone Solar.R Wind Temp Month Day1 41 190 7.4 67 5 12 36 118 8.0 72 5 23 12 149 12.6 74 5 34 18 313 11.5 62 5 46 28 NA 14.9 66 5 67 23 299 8.6 65 5 7
airct <- ctree(Ozone ~ ., data=airq)
airct
Conditional inference tree with 5 terminal nodes Response: Ozone Inputs: Solar.R, Wind, Temp, Month, Day Number of observations: 116 1) Temp <= 82; criterion = 1, statistic = 56.086 2) Wind <= 6.9; criterion = 0.998, statistic = 12.969 3)* weights = 10 2) Wind > 6.9 4) Temp <= 77; criterion = 0.997, statistic = 11.599 5)* weights = 48 4) Temp > 77 6)* weights = 21 1) Temp > 82 7) Wind <= 10.3; criterion = 0.997, statistic = 11.712 8)* weights = 30 7) Wind > 10.3 9)* weights = 7
plot(airct)
결과를 보면 , 최종노드가 5개인 트리모형을 나타낸다 .
위 모형으로부터 새로운 자료에 대한 예측은 predict() 함수를 이용한다.
연속형 반응변수에 대한 예측값은 최종노드에 속한 자료들의 평균값이 제공된다.
분석에 사용된 자료를 재대입한 결과는 다음과 같다 .
head(predict(airct, data=airq))
Ozone[1,] 18.47917[2,] 18.47917[3,] 18.47917[4,] 18.47917[5,] 18.47917[6,] 18.47917
자료가 속하는 해당 최종노드의 번호를 출력하고 싶을 때는 type=”node” 옵션을 사용한다.
predict(airct, data=airq, type="node")
[1] 5 5 5 5 5 5 5 5 3 5 5 5 5 5 5 5 5 5 5 5 5 5 5 6 3 5 6 9 9 6 5 5 5 5 5 8 [37] 8 6 8 9 8 8 8 8 5 6 6 3 6 8 8 9 3 8 8 6 9 8 8 8 6 3 6 6 8 8 8 8 8 8 9 6 [73] 6 5 3 5 6 6 5 5 6 3 8 8 8 8 8 8 8 8 8 8 9 6 6 5 5 6 5 3 5 5 3 5 5 5 6 5[109] 5 6 5 5 3 5 5 5
예측값을 이용하여 평균제곱오차를 구하면 다음과 같다 .
mean((airq$Ozone - predict(airct))^2)
[1] 403.6668
이렇게 해서 의사결정나무에 대해서 알아 보았다 .
아직은 이것이 정확히 어떻게 쓰이면 좋겠다 라는 생각은 안든다 .
그렇지만 의사결정나무를 통해서 어떠한 예측이나 분류 또는 여러가지의 조건들을 수치에 맞게 정리할 수 있을 것 같다 .
그러나 , 의사결정나무는 장점만 있는 것은 아니다.
장점으로는 그 구조가 단순하여 해석이 용이하고 , 유용한 입력변수의 파악과 예측변수간의 상호작용 및 비선형성을 고려하여 분석이 수행되며 , 선형성 , 정규성 , 등분산성 등의 수학적 가정이 불필요한 비모수적 모형이다 .
단점으로는 분류 기준값의 경계선 근방의 자료 값에 대해서는 오차가 클 수 있으며 (비연속성) 로지스틱 회귀와 같이 각 예측변수의 효과를 파악하기 어려우며 , 새로운 자료에 대한 예측이 불안정할 수 있다 .
'졸업작품_preparing.... > 알고리즘' 카테고리의 다른 글
| Metacritic이란 무엇인가 (0) | 2019.01.20 |
|---|---|
| Random Forest는 무엇인가 (0) | 2019.01.14 |
| 결정 트리 학습법이란 무엇인가 (0) | 2019.01.12 |
| Item-based-Filtering 이란 무엇인가 (0) | 2019.01.03 |
| 추천 시스템이란?? (0) | 2018.12.27 |

#IT #먹방 #전자기기 #일상
#개발 #일상
 의사결정나무.R
의사결정나무.R