들어가기 전에 앞서 천체 물리학 협업 네트워크를 다루기 위해서는
저번데 다루었던 페이스북 사용자 네트워크 데이터셋을 다운받은 사이트에서
다운을 받을 수 있다.
천체 물리학 협업 네트워크란 , 어떤 1명의 저자가 논문 1개를 내었을 때 , 혹은 공동작업을 하였을 때 의
ID값들이 서로 연결되어서 네트워크를 이루는 것을 말한다.
1. http://snap.stanford.edu/ <--접속한다
2. Collaboration networks 라는 곳에 들어간다 . 여기서 다루는 것들은 어떤 협력을 통해 이루어진 네트워크들의 데이터를
다룬다는 것으로 생각이 된다.
3.맨 밑에 있는 ca-AstroPh를 다운받아 준다. 아 그리고 다음 페이지에서는 네트워크를 이루는 Nodes , Edegs ... 등등 간단하게
설명을 해주고 있다.
R로 돌아와서 연습을 해본다.
library(igraph)
sn <- read.table(file.choose(), header=F)
# file.choose를 사용해서 임의의 파일을 가져오고 이 파일을 table형식으로 읽어와서 sn에 저장함
head(sn)
# 읽어온 테이블의 head로써 6개 까지 가져온다 // 앞에 부분쪽
tail(sn)
# 읽어온 테이블의 tail로써 6개 까지 가져온다 // 뒤에 부분쪽
sn.df <- graph.data.frame(sn, directed=FALSE)
# graph.data.frame 함으로써 테이블 형식으로 가져온 파일을 방향성없는 데이터프레임을 sn.df에 저장함
plot(sn.df)
# 데이터프레임 형식을 plot으로 차트만듬
# 이 데이터프레임은 데이터가 너무 많아서 오류가 떠서 표현하지 못하였다.... 슬프다.
다음은 특정한 조건을 주어서 그 조건에 맞게 시각화 해볼 것이다. V1 은 ID값이다.
sn1 <- subset(sn, sn$V1==49676)
# sn테이블 파일을 sn$V1 함으로써 V1에 접근하고 49676와 같은 값을 갖는 데이터를 부분집합으로 설정하고 sn1에 그 값을 저장시킴
sn1.df <- graph.data.frame(sn1, directed=FALSE)
# 49676의 값을 부분집합으로 뽑은 데이터를 무방향으로써 데이터프레임 ( sn1.df에 저장시킨다.)
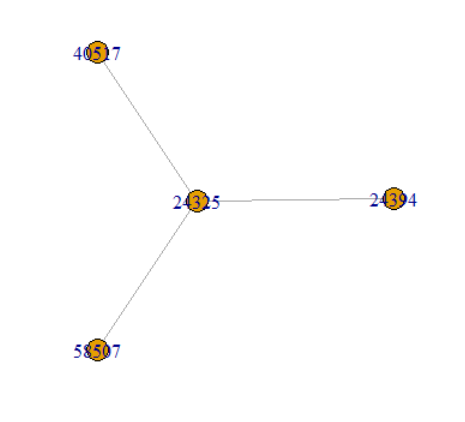
plot(sn1.df)
# 49676의 값을 기준으로한 데이터프레임을 plot으로 뽑는다 .
# 네트워크의 크기: 노드의 총수를 나타나며,
# 페이스북 사용자 데이터 세트는 총 4,039명의 사용자로 구성
vcount(sn.df)
# 노드간의 연결된 edge의 총수,
# 페이스북 사용자간 총 연결수는 총 88,234개로 구성
ecount(sn.df)
# 네트워크에 있는 노들들의 이름
# 모든 노드를 포함하는 노드들의 연속을 만듦
V(sn.df)$name
# 정규화된 연결 정도 중심성
degree(sn.df, normalized=TRUE)
# 이론적인 최대 연결정도 중심
tmax <- centralization.degree.tmax(sn.df)
# 정규화된 연결 정도 중심화
centralization.degree(sn.df, normalized=FALSE)$centralization / tmax
# 노드 중에서 연결정도가 최대인 것
vmax <- V(sn.df)$name[degree(sn.df)==max(degree(sn.df))]
--> V(sn.df)name : 특정한 name값에 접근하려고 할 때 , 연결정도가 최대인 것을 접근하기 위해서 degree(sn.df)와 max(degree(sn.df))값을 같다고 조건을
--> 주는것이다.
# vmax(107)에 해당하는 노드의 연결정도
degree(sn.df, vmax)
# sn.df의 연결정도에 대한 전체적인 정보를 얻을 수 있다.
summary(degree(sn.df))
# 사용자별 연결정도 그래프
plot(degree(sn.df), xlab="사용자 번호", ylab="연결 정도", type='h')
# 연결정도 분포 및 출력
sn.df.dist <- degree.distribution(sn.df)
# 출력결과:
# 연결정도가 작은 노드들이 많고, 연결정도가 큰 노드들은 적은 분포를 나타냄.
# 이러한 모양의 분포를 멱함수 분포라고 하며,
# 네트워크의 많은 분포는 정규분포와는 다르게 멱함수 분포를 띠고 있음
plot(sn.df.dist, xlab="연결 정도", ylab="확률")
# 근접
# 정규화된 근접 중심성
closeness(sn.df, normalized=TRUE)
closeness
# 이론적인 최대 근접 중심성
tmax <- centralization.closeness.tmax(sn.df)
# 정규화된 근접 중심화
centralization.closeness(sn.df, normalized=FALSE)$centralization / tmax
# 정규화된 중개 중심성
betweenness(sn.df, normalized=TRUE)
# p.353
# 이론적인 최대 중개 중심성 및 정규화된 중개 중심성
tmax <- centralization.betweenness.tmax(sn.df)
centralization.betweenness(sn.df, normalized=FALSE)$centralization / tmax
# sn.df에 대한 네트워크 밀도
# 총 연결 정도를 연결 가능한 수로 나눈 비율(1%)
graph.density(sn.df)
# 경로
# 네트워크 경로들에 대한 평균
average.path.length(sn.df)
# sn 데이터 세트에서 사용자 ID가 x보다 작은 ID로 구성된 서브세트를 snx으로 저장
sn10 <- subset(sn, sn$V1<x & sn$V2<x)
# snx 데이터 세트를 igraph 형태의 그래프로 변환
sn10.graph <- graph.data.frame(sn10, directed=FALSE)
# sn10에서의 가장 짧은 경로를 반환함
shortest.paths(sn10.graph)
# y번 사용자와 연결된 최단 경로를 보여 줌
get.shortest.paths(sn10.graph, "y")
# p.355
# x번과 y번 사용자간 최단 경로
get.shortest.paths(sn10.graph, "x", "y")
# x번 사용자가 a번, b번 사용자들과 연결된 각각 최단경로
get.all.shortest.paths(sn10.graph, "x", c("a", "b"))
###############################
'학부공부 > 데이터마이닝과통계' 카테고리의 다른 글
| 기간환율변동 데이터 분석하기 (0) | 2018.10.25 |
|---|---|
| CA-HepTh.txt ( 고에너지 물리학 - 현상학 ) 분석하기 (0) | 2018.10.05 |
| 페이스북 사용자 네트워크 분석 (0) | 2018.09.30 |
| 네트워크만들기 (0) | 2018.09.22 |
| 네트워크의 개요 , 지표 (0) | 2018.09.22 |

#IT #먹방 #전자기기 #일상
#개발 #일상