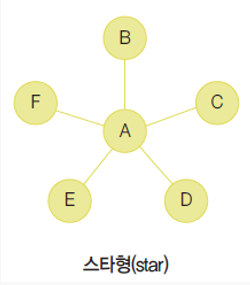
노드를 통해 네트워크를 만들어 보자 .
library(igraph)
# install.packages("igraph")
# igraph 패키지 설치 및 로드
star_1 <-graph(edges = NULL , n =NULL , directed = FALSE)
# n (노드) 와 edges(연결) 이 없고 , 방향 (directed) 가 없는 igraph 생성
star_1 <- star_1 + vertex("A",shape="circle",size=30,color="yellow")
# star_1 그래프에 "A" 노드 추가 , 모양은 원 , 크기는 30 , 색은 노란색
star_1 <- star_1 +vertices("B","C","D","E","F",shape="circle",size=30)
# star_1 그래프에 B,C,D,E,F 노드 추가 모양은 원 , 크기는 30
plot(star_1)
# plot을 통해 vertices 와 node가 잘 만들어 졌는지 확인해 본다.
star_1 <- star_1+edge("A","B")
# star_1 그래프에 노드 연결 ( A 와 B )
star_1 <- star_1+edges("A","C","A","D","A","E","A","F")
# star_1 그래프에 노드 연결 (A와C, A와D, A와E,A와F)
# Degree
degree(star_1,normalized = FALSE)
#star_1 그래프의 연결정도 , normalized = 정규화여부
degree(star_1,normalized = TRUE)
#star_1 그래프의 연결정도 , normalized = 정규화여부
--> 이 결과를 통해서 A에 연결 정도가 강한걸 알 수가 있고 , 정규화를 통해서도 A가 1의 값을 가지며 ,
--> 나머지 B,C,D,E,F가 1의 5분의 1값을 갖는 걸로 보아 A가 중심축인것을 확인할 수 있음
star_max <-centr_degree_tmax(star_1)
star_max
centralization.degree(star_1,normalized = FALSE)$centralization/star_max
# 연결 정도 중심화
# 연결이 한곳으로 집중되면 1에 가깝다
# ------------------Closeness---------------------
closeness(star_1 , normalized = FALSE)
# 각 노드의 근접 중심성
closeness(star_1,normalized = TRUE)
# 각 노드의 정규화된 근접 중심성
# A 는 모든 노드와 1단계로 연결되어 있기 때문에 1
star_max2 <- centralization.closeness.tmax(star_1)
# 근접 중심화의 최대값
centralization.closeness(star_1,normalized = FALSE)$centralization/star_max2
# 정규화된 근접 중심화
# 한 노드에 연결이 집중되어 있음을 의미
#------------------Betweenness--------------------
betweenness(star_1,normalized = FALSE)
#각 노드의 비정규화된 중개 중심성
betweenness(star_1,normalized = TRUE)
#각 노드의 정규화된 중개 중심성
star_max3 <- centralization.betweenness.tmax(star_1)
# 중개 중심화 최댓값
centralization.betweenness(star_1,normalized = FALSE)$centralization /star_max3
# 정규화된 중개 중심화
#----------------------Density--------------------
graph.density(star_1)
# star_1 그래프에 대한 네트워크 밀도
#----------------------최단 경로 -----------------
shortest.paths(star_1)
# 모든 노드에서의 최단 경로를 뽑아줌.
get.shortest.paths(star_1,"A")
# A에서 갈 수 있는 모든 최단 경로를 뽑아줌
# A , A-B , A-B-C , A-B-C-D, A-F-E,A-F
get.shortest.paths(star_1,"A","C")
# A --> C shortest path
get.shortest.paths(star_1,"A",c("C","E"))
# A --> C and A --> E shortest paths
average.path.length(star_1)
# 임의의 두 노드 경로들의 평균 거리
'학부공부 > 데이터마이닝과통계' 카테고리의 다른 글
| 천체 물리학 협업 네트워크를 다뤄보자. (0) | 2018.10.03 |
|---|---|
| 페이스북 사용자 네트워크 분석 (0) | 2018.09.30 |
| 네트워크의 개요 , 지표 (0) | 2018.09.22 |
| 문재인 대통령님의 취임사 데이터 분석하기 (0) | 2018.09.19 |
| 대통령 연설문 텍스트마이닝 해보기 (0) | 2018.09.18 |

#IT #먹방 #전자기기 #일상
#개발 #일상