
201303017_김인우_빅데이터기술
최종발표 자료
목차
Par1.
1. 데이터셋 설명
2. 데이터 분석
3. 알고리즘 적용
4. 수정된 점
5. 최종결과
Part1
데이터셋 설명
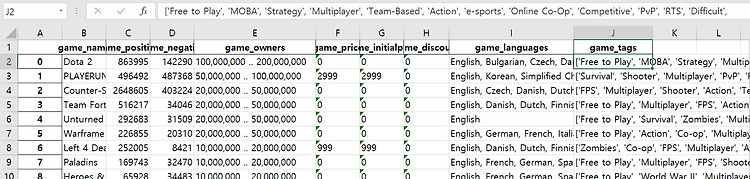
먼저 최종 데이터셋은 다음과 같다.
내가 최종적으로 예측하고자 하는 Y값은 game_price이며, 예측에 필요한 feature들은 다음과 같다.
|
Game_positive(게임의 긍정적인 수), game_negative(게임의 부정적인 수), game_owners(게임 소유자들), game_initialprice(게임 초기가격), game_discount(게임의 할인율) |
왜 게임 가격 예측인가?
게임가격은 소비자들의 입장에서 매우 민감한 부분 중 하나이다. 민감한 부분인만큼 어떠한 부분이 게임가격에 영향을 미치는지 궁금했다.
게임가격을 예측할 수 있다면 굉장히 흥미로울 거라고 생각을 하였다.
어떻게 데이터셋을 수집하였는가?
Steamspyapi를 이용해서 Python에서 api요청을 한뒤 받아온 xml데이터를 가공한 뒤 excel파일로 저장시켜서 데이터를 모았다.
처음에는 staem_game 사이트에서 Scaraping을 하여서 데이터를 모을려고 하였으나, 서버쪽에서 차단을 해서 데이터를 모으기가 힘들었다.
Part1
데이터 분석
이제 본격적으로 코드를 통해서 지금까지 진행했던 부분을 확인해 보겠다.
다음 과정은 game_price를 예측하기 위한 준비단계인 데이터 전처리 단계이다.
먼저, 내가 가지고 있는 데이터셋의 데이터 구조를 확인해야 했다.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import seaborn as sb
import matplotlib.pyplot as plt
기본적인 데이터 구조를 확인하기 위해서 위와 같은 library를 import 해준다.
pd.set_option('display.max_columns', None)
#
DATA_PATH ="C:/Users/user/Desktop/Data/Data.xlsx"
Y_NAME ="game_price"
#
full_dataframe = pd.read_excel(DATA_PATH, sep=',',dtype={'game_owners':int})
#
print(type(full_dataframe))
print("\n* Data Shape : ", full_dataframe.shape)
print("\n* class : ", set(full_dataframe["game_price"].values))
그런 다음 위 코드를 통해서 엑셀파일을 불러와서 데이터의 행과 열을 확인했다.
그리고 내가 예측하고자 하는 game_price의 값들을 class로써 나타내 보았다.
결과값
Data Shape : (29304, 6)
class : {0, 519, 524, 3599, 1039, 529, 1049, ….(중략생략)….1529, 509}
그런 다음 데이터의 구조를 파악해야 했다.
그러기 위해서는 데이터의 null or 공백 or 오탈자를 수정해야 했다.
모든 작업을 노트북으로 작업을 했기 때문에 코드로 돌리는 것이 번거로웠다.
그래서 null or 공백 or 오탈자수정은 엑셀에서 작업을 마쳤다.
그런뒤에 다음 코드를 통해서 null 값을 확인해 보았다.
# # 결측치 확인
print("결측치 확인")
print(full_dataframe[full_dataframe.isnull().any(1)])
결과값
결측치 확인
Empty DataFrame
위 과정이 끝났다고 생각을 하여서 내가 예측하고자 하는 game_price의 class들의 비중을 확인해 보았다.
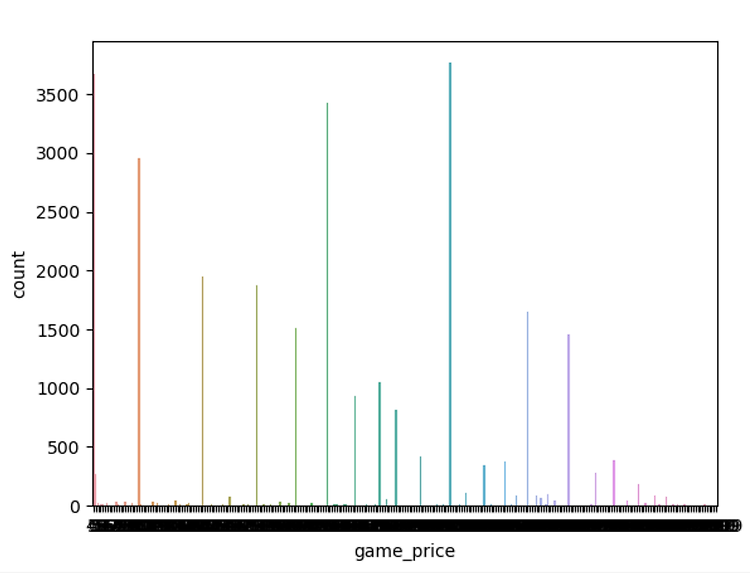
# # Data balance 확인 ( price의 비중을 시각화해서 확인해 보인다 )
sb.countplot(x=Y_NAME, data=full_dataframe)
plt.show()
결과값

시각화를 하였는데 정확한 수치를 알 수 없었기 때문에 수치로 알아보고자 다음 코드로 확인해 보았다.
# # Data balance 확인2 ( 카운트별로 갯수와 비중확인 )
labels_count = dict(game_price=0)
labels_count2 = {}
#
count = []
total = 0
print(labels_count)
print(*np.unique(full_dataframe[Y_NAME], return_counts=True))
for label in full_dataframe[Y_NAME].values:
if label in labels_count2:
labels_count2[label] +=1
else:
labels_count2[label] =1
for count in labels_count2.values():
total += count
print(total)
for label in labels_count2.items():
print("{0: <15} 개수:{1}개\t데이터비중:{2:.3f}".format(*label, label[1]/total))
del labels_count2
위 코드는 game_price의 각 값에 따른 데이터비중을 수치화로 나타내 본 것이다.
결과값은 다음과 같았다.
0 개수:3678개 데이터비중:0.126
2999 개수:383개 데이터비중:0.013
999 개수:3767개 데이터비중:0.129
499 개수:3432개 데이터비중:0.117
1999 개수:1461개 데이터비중:0.050
3959 개수:2개 데이터비중:0.000
1499 개수:1648개 데이터비중:0.056
799 개수:812개 데이터비중:0.028
3499 개수:49개 데이터비중:0.002
299 개수:1877개 데이터비중:0.064
399 개수:1514개 데이터비중:0.052
1299 개수:381개 데이터비중:0.013
2499 개수:283개 데이터비중:0.010
위 결과값을 통해서 각 game_price의 각각의 값들의 데이터비중을 알 수 있었다
데이터의 비중을 확인하였고, Resampling을 하다가 잘 해결되지 않아서 Resampling은 진행하지 않았다.
그리고 feature selection 을 통해서 내게 주어진 데이터셋중 어떤 것을 택해서 해야할지 고민을 해보았다.
Feature_selection도 종류가 다양했는데 나는 다 해보았다.
각각의 feature_selection을 확인해 본다.
Feature_selection(1)
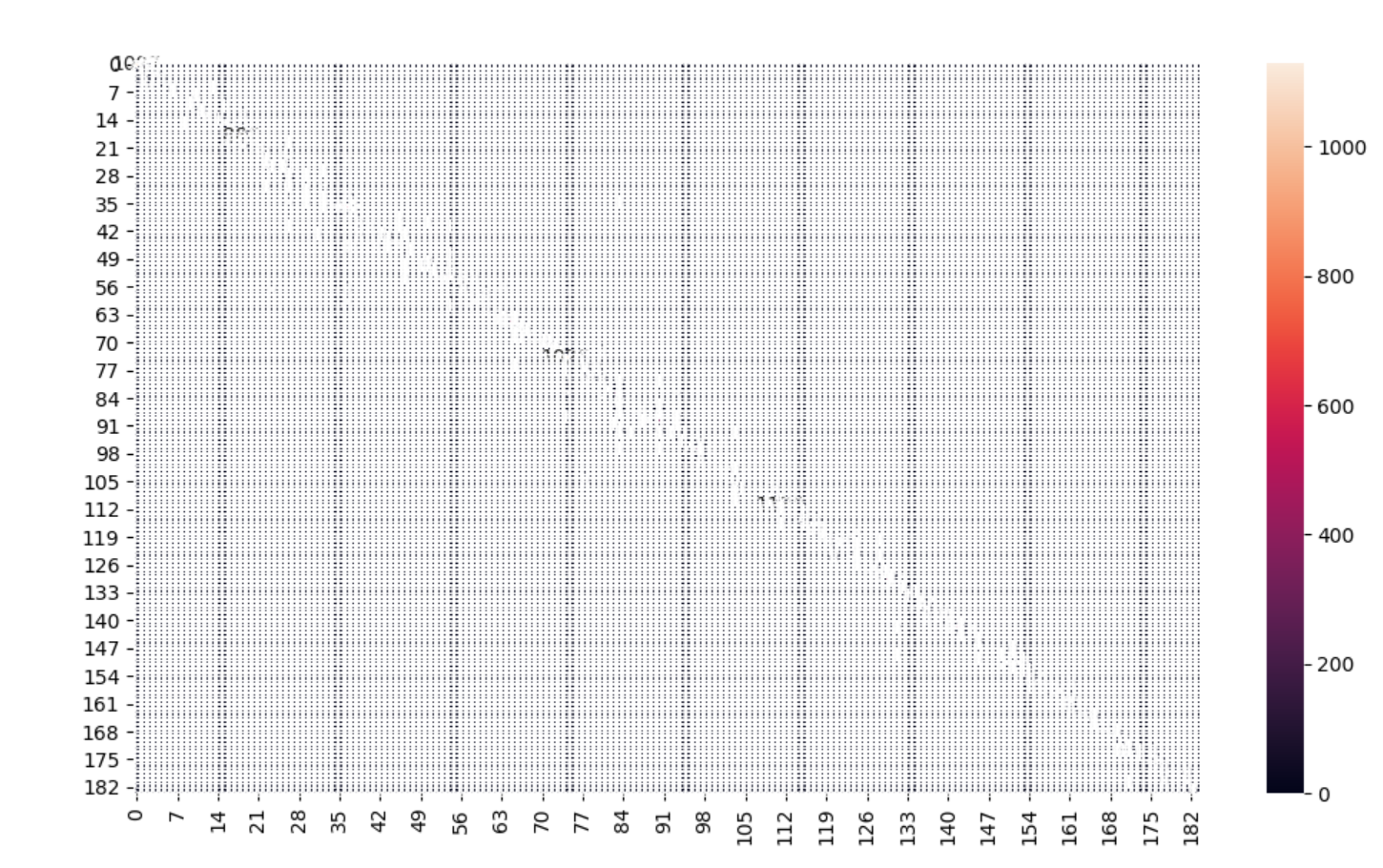
# Feature selection with correlation and random forest classificatio (1)
f,ax = plt.subplots(figsize=(18,18))
sns.heatmap(full_dataframe.corr(), annot=True, linewidths=.5, fmt='.1f',ax=ax)
plt.show()
결과값

데이터의 비중을 눈으로 쉽게 확인할 수 있었다.
눈으로 확인이 되었으니까 수치로 보고싶었다.
다음 코드를 통해서 수치를 확인했다.
# split data train 70% and test 30%
# X_train, X_test, y_train, y_test = train_test_split(full_dataframe, full_dataframe[Y_NAME], test_size=0.3, random_state=42)
# random forest clssifier with n_estimators=10 (default)
clf_rf = RandomForestClassifier(random_state=43)
clr_rf = clf_rf.fit(X_train,y_train)
ac = accuracy_score(y_test,clf_rf.predict(X_test))
print("random forest clssifier")
print('Accuracy is: ',ac)
RandomForestClassifier를 통해서 정확도를 다음처럼 구할 수 있었다.
결과값
random forest clssifier
Accuracy is: 0.9783894449499545
높은 점수처럼 보이지만, 썩 신뢰가 가진 않는다.
그래서 다른 feature selection을 해보았다.
feature_selection(2)
# Univariate feature selection and random forest classification (2)
# find best scored 5 features
select_feature = SelectKBest(chi2, k=5).fit(X_train, y_train)
print("find best scored 5 features")
print('Score list : ', select_feature.scores_)
print('Feature list : ', X_train.columns)
# best 5 features
x_train2 = select_feature.transform(X_train)
x_test2 = select_feature.transform(X_test)
# random forest classifier with n_estimators=10 (default)
clf_rf_2 = RandomForestClassifier()
clr_rf_2 = clf_rf_2.fit(x_train2,y_train)
ac_2 = accuracy_score(y_test,clf_rf_2.predict(x_test2))
print("Accuracy is : ", ac_2)cm_2 = confusion_matrix(y_test,clf_rf_2.predict(x_test2))
sns.heatmap(cm_2,annot=True,fmt="d")
plt.show()
결과값
Score list : [4.32081632e+07 2.55317959e+07 2.51462733e+09 3.04421518e+07
3.13432396e+07 6.54490938e+05]
Feature list : Index(['game_positive', 'game_negative', 'game_owners', 'game_price',
'game_initialprice', 'game_discount'],
dtype='object')
Accuracy is : 0.9740673339399454
위 결과값을 통해서 정확도와 feature_list와 score_list를 알 수 있었다.
그렇지만 이정보로는 부족하다.
feature_selection(3)
# Recursive feature elimination (RFE) with random forest ( 3 )
# Create the RFE object and rank each pixel
clf_rf_3 = RandomForestClassifier()
rfe = RFE(estimator=clf_rf_3, n_features_to_select=5, step=1)
rfe = rfe.fit(X_train, y_train)
print("RFE")
print("Chosen best 5 feature by rfe : ", X_train.columns[rfe.support_])
결과값
RFE
Chosen best 5 feature by rfe : Index(['game_positive', 'game_negative', 'game_price', 'game_initialprice',
'game_discount'],
dtype='object')
è By rfe에 의해서 선별되어진 best 5를 알 수 있었다.
feature_selection(4)
# Recursive feature elimination with cross validation and random forest classification ( 4 )
# The "accuracy" scoring is proportional to the number of correct classifications
clf_rf_4 = RandomForestClassifier()
rfecv = RFECV(estimator=clf_rf_4, step=1, cv=5, scoring='accuracy')
rfecv = rfecv.fit(X_train, y_train)
#
print("Recursive feature elimination")
print('Optimal number of features :', rfecv.n_features_)
print('Best features :', X_train.columns[rfecv.support_])
결과값
Recursive feature elimination
Optimal number of features : 1
Best features : Index(['game_price'], dtype='object')
è Recursive feature elimination에 의한 결과값은 game_price 1개가 나왔다.
feature_selection(5)
# Tree based feature selection and random forest classification ( 6 )
clf_rf_5 = RandomForestClassifier()
clr_rf_5 = clf_rf_5.fit(X_train,y_train)
importances = clr_rf_5.feature_importances_
std = np.std([tree.feature_importances_ for tree in clf_rf.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
# Print the feature ranking
print("Feature ranking:")
for f in range(X_train.shape[1]):
print("%d. feature %d (%f)" % (f + 1, indices[f], importances[indices[f]]))
# Plot the feature importances of the forest
print("Plot the feature importance")
plt.figure(1, figsize=(14, 13))
plt.title("Feature importances")
plt.bar(range(X_train.shape[1]), importances[indices],
color="g", yerr=std[indices], align="center")
plt.xticks(range(X_train.shape[1]), X_train.columns[indices], rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.show()
결과값

Feature ranking:
1. feature 4 (0.498833)
2. feature 3 (0.434810)
3. feature 5 (0.027699)
4. feature 0 (0.018487)
5. feature 1 (0.015815)
6. feature 2 (0.004356)
Plot the feature importance
è 개인적으로 이 feature_selection이 제일 좋았다. 그래프로 찍음으로써 데이터의 중요도를 쉽게 볼 수 있으며 , 수치로도 확인이 가능하기 때문이다.
è game_initialprice가 feature 중요도가 제일 높았다.
Feature_selection은 이렇게 5가지를 해보았으며 마지막 5번이 제일 좋았다. 눈으로 보기 제일 쉽고, 수치로도 나오기 때문이다.
이제 scaling을 해보겠다.
나는 scaling 4가지 ( Minmax,standard,Robust,Normalizer ) 를 다해보았으며 각각을 코드를 통해서 확인해 보겠다.
(1) StandardScaler Code
# (1) StandardScaler code
scaler = StandardScaler()
X_train_scale = scaler.fit_transform(X_train)
print("StandardScaler code")
print('스케일 조정 전 feature Min value : \n {}'.format(X_train.min(axis=0)))
print('스케일 조정 전 feature Max value : \n {}'.format(X_train.max(axis=0)))
print('스케일 조정 후 feature Min value : \n {}'.format(X_train_scale.min(axis=0)))
print('스케일 조정 후 feature Max value : \n {}'.format(X_train_scale.max(axis=0)))
결과값
StandardScaler code
스케일 조정 전 feature Min value :
game_positive 0
game_negative 0
game_owners 10000
game_price 0
game_initialprice 0
game_discount 0
dtype: int64
C:\Users\user\PycharmProjects\machinelearning\venv\lib\site-packages\sklearn\base.py:464: DataConversionWarning: Data with input dtype int32, int64 were all converted to float64 by StandardScaler.
return self.fit(X, **fit_params).transform(X)
스케일 조정 전 feature Max value :
game_positive 2648605
game_negative 487368
game_owners 150000000
game_price 39999
game_initialprice 39999
game_discount 90
dtype: int64
스케일 조정 후 feature Min value :
[-0.04886008 -0.04601326 -0.08081543 -0.71240348 -0.70940402 -0.25357541]
스케일 조정 후 feature Max value :
[124.88592683 100.37860636 116.56060055 37.1192881 34.72217609
5.79918511]
à 위를 통해 스케일 조정 후 값의 변화가 생긴 것을 확인 할 수 있다.
(2) Robustscaler code
# RobustScaler code
scaler = RobustScaler()
X_train_scale2 = scaler.fit_transform(X_train)
print("RobustScaler code")
print('스케일 조정 전 feature Min value : \n {}'.format(X_train.min(axis=0)))
print('스케일 조정 전 feature Max value : \n {}'.format(X_train.max(axis=0)))
print('스케일 조정 후 feature Min value : \n {}'.format(X_train_scale2.min(axis=0)))
print('스케일 조정 후 feature Max value : \n {}'.format(X_train_scale2.max(axis=0)))
결과값
스케일 조정 전 feature Min value :
game_positive 0
game_negative 0
game_owners 10000
game_price 0
game_initialprice 0
game_discount 0
dtype: int64
스케일 조정 전 feature Max value :
game_positive 2648605
game_negative 487368
game_owners 150000000
game_price 39999
game_initialprice 39999
game_discount 90
dtype: int64
스케일 조정 후 feature Min value :
[-0.2 -0.21052632 0. -0.62375 -0.62375 0. ]
스케일 조정 후 feature Max value :
[23031.14782609 12825.26315789 9999.33333333 49.375
49.375 90. ]
(3) Minmaxscaler code
scaler = MinMaxScaler()
X_train_scale3 = scaler.fit_transform(X_train)
print("MinMaxScaler code")
print('스케일 조정 전 features Min value : \n {}'.format(X_train.min(axis=0)))
print('스케일 조정 전 features Max value : \n {}'.format(X_train.max(axis=0)))
print('스케일 조정 후 features Min value : \n {}'.format(X_train_scale3.min(axis=0)))
print('스케일 조정 후 features Max value : \n {}'.format(X_train_scale3.max(axis=0)))
결과값
스케일 조정 전 features Min value :
game_positive 0
game_negative 0
game_owners 10000
game_price 0
game_initialprice 0
game_discount 0
dtype: int64
스케일 조정 전 features Max value :
game_positive 2648605
game_negative 487368
game_owners 150000000
game_price 39999
game_initialprice 39999
game_discount 90
dtype: int64
스케일 조정 후 features Min value :
[0. 0. 0. 0. 0. 0.]
스케일 조정 후 features Max value :
[1. 1. 1. 1. 1. 1.]
(4) Normalizer
scaler = Normalizer()
X_train_scale4 = scaler.fit_transform(X_train)
print("Normalizer code")
print('스케일 조정 전 feature Min value : \n {}'.format(X_train.min(axis=0)))
print('스케일 조정 전 feature Max value : \n {}'.format(X_train.max(axis=0)))
print('스케일 조정 후 feature Min value : \n {}'.format(X_train_scale4.min(axis=0)))
print('스케일 조정 후 feature Max value : \n {}'.format(X_train_scale4.max(axis=0)))
결과값
스일 조정 전 feature Min value :
game_positive 0
game_negative 0
game_owners 10000
game_price 0
game_initialprice 0
game_discount 0
dtype: int64
스일 조정 전 feature Max value :
game_positive 2648605
game_negative 487368
game_owners 150000000
game_price 39999
game_initialprice 39999
game_discount 90
dtype: int64
스일 조정 후 feature Min value :
[0. 0. 0.17408188 0. 0. 0. ]
스일 조정 후 feature Max value :
[0.15103973 0.12033541 1. 0.6963101 0.93654483 0.00898835]
이렇게 각각의 scaling을 적용시켜봄으로써 전과 후의 데이터값의 변화를 살펴 보았다.
SVC모델을 적용시켜서 어떤 scaling이 정확도의 차이가 큰지 확인해 보았다.
svc = SVC()
svc.fit(X_train, y_train)
print("적용전")
print('test accuracy : %3f' %(svc.score(X_test, y_test)))
# # 적용 시킨 후 (1)
scaler_min = StandardScaler()
X_train_scale5 = scaler_min.fit_transform(X_train)
X_test_scale = scaler_min.transform(X_test)
svc.fit(X_train_scale5, y_train)
print("적용후 ")
print('Scaled test accuracy : %.3f' %(svc.score(X_test_scale,y_test)))
내가 가지고 있는 데이터셋에는 StandardScaler가 SVC 모델을 통해 적용시키기 전과 후의 값의 차이가 제일 컸으며 제일 score가 높았다. 그래서 나는 standardScaler를 사용해야 겠다라고 생각하였다.
# MinMaxScaler : 0.640 --> 0.262
# StandardScaler : 0.640 --> 0.932
# RobustScaler : 0.640 --> 0.843
# Normalizer : 0.640 --> 0.294
Part1
알고리즘 적용
중간 발표때의 목표는 Linear-regresson 을 사용해서 Game_price를 예측하려고 하였다.
그러나, Linear-regression 하나로는 나의 예측이 정확한지 알 수 없었으며, 또한 이 알고리즘이 맞는지 혹은 데이터의 예측이 제대로 된것인지 알수가 없었다.
그래서 다음 사이트에서 regressor를 사용할수 있는 알고리즘을 9개 정도 찾아서 적용해 보았다.
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.tree
다음은 알고리즘적용에 필요한 library 를 먼저 import 해준다.
import pandas as pd
import numpy as np
import statsmodels.api as sm
from sklearn import linear_model
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# DecisionTreeRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
# Evaluating the Algorithm
from sklearn import metrics
# GradientBoostingRegressor
from sklearn.ensemble import GradientBoostingRegressor,BaggingRegressor,RandomForestRegressor
# AdaBoostRegressor
from sklearn.ensemble import AdaBoostRegressor
# Dummy estimators
from sklearn.dummy import DummyRegressor
# Gaussian Proecesses
from sklearn.gaussian_process import GaussianProcessRegressor
# neural_network.MLPRegressor
from sklearn.neural_network import MLPRegressor
알고리즘 설명에 앞서 , random_state 의 값을 43과 0으로 2번돌려본 뒤 결과값의 차이를 알아 보았다.
사전에 진행할 때는 random_state의 값이 데이터예측에 큰 영향을 안 미치는줄 알았다.
그러나, 이 생각은 잘못된 생각이였다.
그래서 random_state의 값을 0과 43으로 하이퍼매개변수를 변경해본 뒤 비교해 보았다.
다음은 진행한 9가지 알고리즘을 하나씩 코드를 보면서 설명해 보겠다.
9가지 알고리즘을 비교할 때 다음의 값들을 비교해서 최적의 알고리즘을 선별해 보았다.
Mean Absolute Error
Mean Squared Error
Root Mean Squared Error
Accuracy
R-squared for Train
R-squared for Test
위의 6개의 변수를 사용한 이유는 한가지가 있다.
나는 나의 데이터를 가지고 알고리즘에 적용을 해야했고, 제일 괜찮은 알고리즘을 선별해서
적용해야 했다.
그러기 위해서는 알고리즘을 구별할 수 있는 수치가 필요했다.
그러다가 알게된 것이 metric 함수 였다.
sklearn에서 제공하는 함수였으며 regressor에서 사용되었다.
최대한 많이 써서 비교해 볼려고 6개 정도 뽑아보았지만
그나마 이해가 되는
Mean Absolute Error
Accuracy
R-squared for Train
R-squared for Test
위의 4가지를 가지고 알고리즘을 비교해 보았다.
참고바란다.
|
Mean Absolute Error : 예측하는 값에 대한 위험도 Mean Squared Error : 제곱근에 대한 손실 예상값 Root Mean Squared Error : 평균제곱근 편차들을 하나의 측도로 예측할 때 Accurary : 각 알고리즘에 대한 정확도 R-quared for Train : 훈련데이터에 대한 제곱근 값 R-squared for test : 테스트데이터에 대한 제곱근 값 |
(1)LinearRegression
à random_state = 43 으로 설정해서 결과값을 뽑아보았다.
# ---------------------------- LinearRegression
# split data train 70% and test 30%
X_train, X_test, y_train, y_test = train_test_split(full_dataframe, full_dataframe[Y_NAME], test_size=0.3, random_state=43)
# test_size = 0.3 을 하게되면 test_Data 가 30% 비중을 차지하게 되고 , 자동으로 train_data가 70%로 적용이 된다
# random_state=0으로 두는것은 위험.
# 그래서 random_state가 0일때와 43일때 두가지 경우를 구해보았다.
im = linear_model.LinearRegression()
# LinearRegression()을 사용하기 위해서 변수 im에 저장시킨다.
model = im.fit(X,y)
# LinearRegression에 나의 데이터셋을 fit시킨다.
prediction_linear = im.predict(X)
# 알고리즘의 predict를 나의 데이터셋 X를 사용해서 예측한다.
# # 예측값과 실제값을 비교
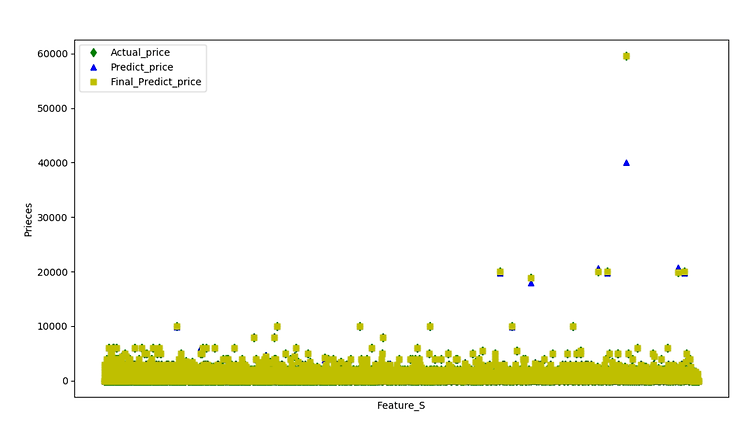
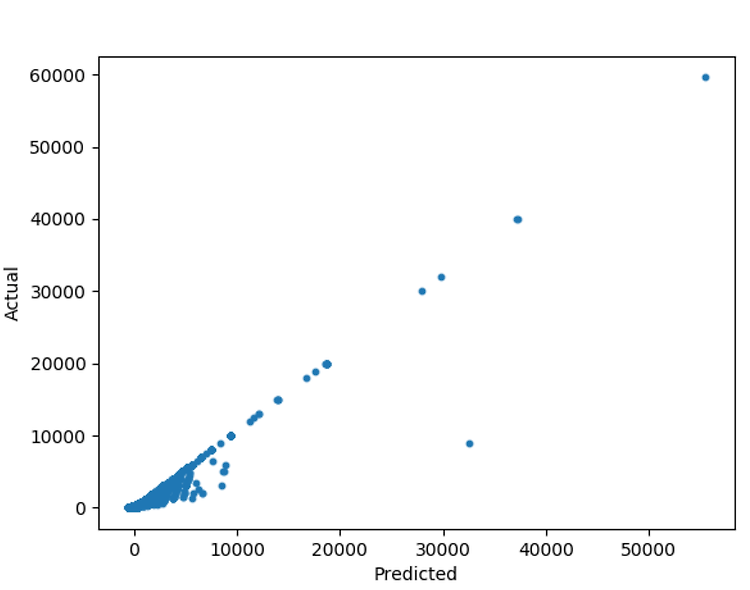
plt.scatter(prediction_linear,y,s=10)
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.show()
print("coef :"+str(im.coef_))
print("score :"+str(im.score(X,y)))
print("intercept :"+str(im.intercept_))
print("Actual price : "+ str(y))
print("predict price :"+str(prediction_linear))
LinearRegression_결과값
coef :[-6.58419961e-05 1.59727445e-04 1.29593935e-07 9.30383123e-01
-1.16008179e+01]
score :0.9566722956471095
intercept :53.1834889494703
저는 예측하기 전의 가격과 알고리즘 적용 후의 가격의 변동이 어떻게 되는지 다음처럼 결과를 출력해보았다.
위의 결과를 바탕으로 score점수가 높게 나왔지만, 실질적으로 f1-score처럼 계산한 것이 아니기 때문에 결과값만 높게 출력된 것이다.
Actual price predict price
0 0 38.463042
1 2999 2895.686163
2 0 -53.560163
3 0 27.872660
4 0 42.185356
결과값을 보면 똑 같은 0의 값이 여러 개의 값으로 예측이 되는 것을 알 수 있다.
이를 통해서 Linear_regression은 엄청 정확한 예측은 아니다 라고 결론을 내릴 수 가 있었다.
그리고 예측을 통해 소수점 자리의 처리와 값의 오차 범위를 지정해야 했다.
오차 범위와 소수점 자리의 처리를 하기 전에 좀 더 정확한 알고리즘을 사용하면 이 작업을 좀 더 손쉽게 할 수 있지 않을까라고 생각했다.
그래서 다른 알고리즘을 더 설명해 보겠다.
(2)DecisionTreeRegressor
# --------------------------DecisionTreeRegressor
regressor = DecisionTreeRegressor()
# DecisionTreeRegressor() 함수를 만든다.
regressor.fit(X_train,y_train)
# 위에서 나누어준 훈련데이터를 DecisionTreeRegressor에 fit시킨다.
# To make predictions on the test set, uses the predict method
y_pred = regressor.predict(X_test)
# 위에서 나누어준 테스트데이터에 DecisionTreeRegressor로 예측을 한다.
df = pd.DataFrame({'Actual':y_test, 'Predicted':y_pred})
print(df)
# 알고리즘 적용전의 가격과 알고리즘 적용 후의 가격을 비교하고 싶어서 print로 출력.
# # mean_absolute_error 함수는 평균 절대 오류, 절대 오류 손실 또는 기대치 손실의 예상 값에 해당하는 위험 메트릭을 계산합니다.
print('DecisionTreeRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,y_pred))
# # mean_squared_log_error 함수는 제곱 된 로그 (2 차) 오류 또는 손실의 예상 값에 해당하는 위험 메트릭을 계산합니다.
print('DecisionTreeRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,y_pred))
# # 평균 제곱근 편차 또는 평균 제곱근 오차는 추정 값 또는 모델이 예측한 값과 실제 환경에서
# # 관찰되는 값의 차이를 다룰 떄 흔히 사용하는 측도이다.
# # 정밀도를 표현하는데 적합하다.
# # 각각의 차이값은 잔차라고도 하며, 평균 제곱근 편차들을 하나의 측도로 종합할 때 사용된다.
print('DecisionTreeRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,y_pred)))
print('DecisionTreeRegressor Accuracy:', metrics.r2_score(y_test,y_pred))
# R-squared : 제곱근을 의미하는데 1에 가까울 정확한 값을 의미
print("DecisionTreeRegressor R-squared for Train: %.2f" %regressor.score(X_train,y_train))
print("DecisionTreeRegressor R-squared for Test: %.2f" %regressor.score(X_test,y_test))
DecisionTreeRegressor 결과값
#random_state=0 일때
# DecisionTreeRegressor Mean Absolute Error: 0.7187215650591446
# DecisionTreeRegressor Mean Squared Error: 1396.9334622383985
# DecisionTreeRegressor Root Mean Squared Error: 37.375573069029976
# DecisionTreeRegressor Accuracy: 0.9984125399095579
# random_state=43일때
# DecisionTreeRegressor Mean Absolute Error: 2.4709963603275704
# DecisionTreeRegressor Mean Squared Error: 43819.10111464968
# DecisionTreeRegressor Root Mean Squared Error: 209.33012471846874
# DecisionTreeRegressor Accuracy: 0.9673605977859902
# DecisionTreeRegressor R-squared for Train: 1.00
# DecisionTreeRegressor R-squared for Test: 0.97
위 결과값을 바탕으로 DecisionTreeRegressor은 나름 정확하게 예측이 되었다고 생각이 들었다.
또한 random_state의 숫자에 따른 다른 결과값이 나왔음 또한 알 수 있었다.
훈련데이터에 대한 알고리즘 제곱근은 1에 일치했으며, 테스트데이터에 대한 알고리즘 제곱근은 0.97로써 정말 높은 수치를 나타냈다.
(3) Gradientboostingregresoor
# -----------------------------Gradientboostingregressor
gbrt = GradientBoostingRegressor()
# GradientBoostingRegressor 선언
gbrt.fit(X_train,y_train)
# 나의 데이터를 GradientBoostingRegressor에 적용시킨다.
gbrt_y_pred = gbrt.predict(X_test)
# GradientBoostingRegressor 알고리즘을 통해 Y를 예측한다.
print("Feature importances")
print(gbrt.feature_importances_)
# GradientBoostingRegressor 메소드중 feature 중요도를 나타내는 것이 있었다.
print('Gradientboostingregressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,gbrt_y_pred))
print('Gradientboostingregressor Mean Squared Error:', metrics.mean_squared_error(y_test,gbrt_y_pred))
print('Gradientboostingregressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,gbrt_y_pred)))
print('Gradientboostingregressor Accuracy:', metrics.r2_score(y_test,gbrt_y_pred))
# 예측 전의 Y 값과 예측 후의 Y값
gbrt_df = pd.DataFrame({'Actual':y_test, 'Predicted':gbrt_y_pred})
print(gbrt_df)
# 훈련데이터와 테스트데이터 각각의 알고리즘에 대한 정확도
print("R-squared for Train: %.2f" %gbrt.score(X_train,y_train))
print("R-squared for Test: %.2f" %gbrt.score(X_test,y_test))
Gradientboostingregresoor 결과값
# random_state=0일때
# Gradientboostingregressor Mean Absolute Error: 0.7922192368407802
# Gradientboostingregressor Mean Squared Error: 16.667078349470625
# Gradientboostingregressor Root Mean Squared Error: 4.082533324967553
# Gradientboostingregressor Accuracy: 0.9999810597122775
# R-squared for Train: 1.00
# R-squared for Test: 1.00
# random_state=43일때
# Gradientboostingregressor Mean Absolute Error: 2.9070040004338233
# Gradientboostingregressor Mean Squared Error: 43876.08301832946
# Gradientboostingregressor Root Mean Squared Error: 209.46618585902942
# Gradientboostingregressor Accuracy: 0.9673181538465707
# R-squared for Train: 1.00
# R-squared for Test: 0.97
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 0.219401
27293 1399 1404.371912
26497 1599 1599.359166
25231 49 49.652013
1364 99 99.031378
7691 0 0.219401
19177 99 99.031378
22706 399 399.292501
위의 결과값을 통해 그래디언트부스팅 또한 훈련데이터와 테스트데이터의 알고리즘 정확도 수치가 높게 나왔다. Absolute Error의 결과값 또한 낮게 나온 것을 확인하였다.
위를 통해 알 수 있듯이 전의 가격과 소수점 아래자리가 다른 것 말고는 정확하게 예측했음을 알 수 있었다.
(4)AdaBoostRegressor
# -----------------------------------AdaBoostRegressor
abr = AdaBoostRegressor()
# AdaBoostRegressor 알고리즘 선언
abr.fit(X_train,y_train)
# AdaBoostRegressor 알고리즘에 나의 데이터를 적용시킨다.
abr_y_pred = abr.predict(X_test)
# AdaBoostRegressor 알고리즘을 사용하여서 Y값을 예측한다
#
print('AdaBoostRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,abr_y_pred))
print('AdaBoostRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,abr_y_pred))
print('AdaBoostRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,abr_y_pred)))
print('AdaBoostRegressor Accuracy:', metrics.r2_score(y_test,abr_y_pred))
abr_df = pd.DataFrame({'Actual':y_test, 'Predicted':abr_y_pred})
print(abr_df)
print("R-squared for Train: %.2f" %abr.score(X_train,y_train))
print("R-squared for Test: %.2f" %abr.score(X_test,y_test))
AdaBoostRegressor 결과값
# ------------------------------------------- Output
# random_state=0일때
# AdaBoostRegressor Mean Absolute Error: 264.095934658306
# AdaBoostRegressor Mean Squared Error: 105842.9302694874
# AdaBoostRegressor Root Mean Squared Error: 325.3351045760162
# AdaBoostRegressor Accuracy: 0.8797212378397619
# R-squared for Train: 0.92
# R-squared for Test: 0.88
# random_state=43일때
# AdaBoostRegressor Mean Absolute Error: 262.2391348191739
# AdaBoostRegressor Mean Squared Error: 131324.9843951394
# AdaBoostRegressor Root Mean Squared Error: 362.38789217513795
# AdaBoostRegressor Accuracy: 0.9021803533758822
# R-squared for Train: 0.92
# R-squared for Test: 0.90
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 316.362836
27293 1399 1363.562170
26497 1599 1363.609208
25231 49 316.362836
1364 99 316.362836
7691 0 316.362836
19177 99 316.362836
22706 399 421.849131
AdaboostRegressor의 결과값으로 미루어 보아, Absolute의 수치는 조금 높은 편이였고 정확도는 0.9 정도 였으며 훈련데이터와 테스트데이터의 정확도는 0.9~0.92 사이였다. 그래도 나름 정확한 예측이라고 생각을 하였다.
그런데 예측하기 전의 price 가격과 예측 후의 가격의 변동을 보면 위처럼 정확하지 않은 데이터가 보이는 것을 확인할 수 있었다.
(5)DummyRegressor
# -----------------------------------DummyRegressor
Dummy = DummyRegressor()
# DummyRegressor 알고리즘 선언
Dummy.fit(X_train,y_train)
# DummyRegressor 알고리즘에 나의 데이터를 적용시켜본다.
Dummy_y_pred = Dummy.predict(X_test)
# Dummy 알고리즘을 사용해서 Y값을 예측한다.
#
print('DummyRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,Dummy_y_pred))
print('DummyRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,Dummy_y_pred))
print('DummyRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,Dummy_y_pred)))
print('DummyRegressor Accuracy:', metrics.r2_score(y_test,Dummy_y_pred))
Dummy_df = pd.DataFrame({'Actual':y_test, 'Predicted':Dummy_y_pred})
print(Dummy_df)
print("R-squared for Train: %.2f" %Dummy.score(X_train,y_train))
print("R-squared for Test: %.2f" %Dummy.score(X_test,y_test))
DummyRegressor 결과값
# random_state=0일 때
# DummyRegressor Mean Absolute Error: 603.3633884521669
# DummyRegressor Mean Squared Error: 880156.477329049
# DummyRegressor Root Mean Squared Error: 938.1665509540665
# DummyRegressor Accuracy: -0.00020030937269321925
# R-squared for Train: 0.00
# R-squared for Test: -0.00
# random_state=43일 때
# DummyRegressor Mean Absolute Error: 606.3160356253877
# DummyRegressor Mean Squared Error: 1342621.3396696597
# DummyRegressor Root Mean Squared Error: 1158.7153833749078
# DummyRegressor Accuracy: -7.432402441365227e-05
# R-squared for Train: 0.00
# R-squared for Test: -0.00
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 757.948469
27293 1399 757.948469
26497 1599 757.948469
25231 49 757.948469
1364 99 757.948469
7691 0 757.948469
19177 99 757.948469
DummyRegressor 알고리즘은 나의 데이터셋에 안맞는 알고리즘이였다.
Absolute Error 수치도 조금 높은 편이였고, 알고리즘에 대한 수치도 – 수치가 나왔으며 , 훈련데이터와 테스트데이터를 알고리즘에 적용한 값 또한 0에 가까운 수치였다.
그래서 Actual 과 predict의 결과값 또한 이상하게 나오겠다 라고 생각을 하였는데, 역시나 위처럼 가격의 예측이 이상하게 나왔었다.
(6)BaggingRegressor
# ---------------------------------BaggingRegressor
bagg = BaggingRegressor()
# BaggingRegressor 알고리즘 선언
bagg.fit(X_train,y_train)
# BaggingRegressor 알고리즘에 나의 데이터를 적용시킨다.
bagg_y_pred = bagg.predict(X_test)
# BaggingRegressor 알고리즘을 사용해서 Y를 예측한다.
print('BaggingRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,bagg_y_pred))
print('BaggingRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,bagg_y_pred))
print('BaggingRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,bagg_y_pred)))
print('BaggingRegressor Accuracy:', metrics.r2_score(y_test,bagg_y_pred))
bagg_df = pd.DataFrame({'Actual':y_test, 'Predicted':bagg_y_pred})
print(bagg_df)
print("R-squared for Train: %.2f" %bagg.score(X_train,y_train))
print("R-squared for Test: %.2f" %bagg.score(X_test,y_test))
BaggingRegressor 결과값
# random_state=0일때
# BaggingRegressor Mean Absolute Error: 0.7531505914467703
# BaggingRegressor Mean Squared Error: 404.7560202456782
# BaggingRegressor Root Mean Squared Error: 20.11854915856703
# BaggingRegressor Accuracy: 0.9995400396326132
# R-squared for Train: 0.99
# R-squared for Test: 1.00
# random_state=43일때
# BaggingRegressor Mean Absolute Error: 2.7680391264786173
# BaggingRegressor Mean Squared Error: 52422.568587352136
# BaggingRegressor Root Mean Squared Error: 228.95975320425234
# BaggingRegressor Accuracy: 0.960952158814548
# R-squared for Train: 1.00
# R-squared for Test: 0.96
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 0.0
27293 1399 1399.0
26497 1599 1599.0
25231 49 49.0
1364 99 99.0
7691 0 0.0
19177 99 99.0
22706 399 399.0
BaggingRegressor 알고리즘을 사용해서 확인 해본 결과 BaggingRegressor 알고리즘에 대한 정확도는 0.96, 훈련데이터와 테스트데이터의 수치 값 각각 1.0,0.96 이였고, Absolute Error 의 값은 2.7정도였다.
나름 정확한 알고리즘이였는데 알고리즘예측 전의 가격과 알고리즘예측 후의 가격을 확인해 본 결과 예측이 어느 정도 맞아 떨어졌다.
(7)RandomForestRegressor
# --------------------------RandomForestRegressor
RanDF = RandomForestRegressor()
# RandomForestRegressor 알고리즘 선언
RanDF.fit(X_train,y_train)
# RandomForestRegressor 알고리즘에 나의 데이터를 적용시킨다.
RanDF_y_pred = RanDF.predict(X_test)
# BaggingRegressor 알고리즘을 사용해서 Y값을 예측한다.
print('RandomForestRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,RanDF_y_pred))
print('RandomForestRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,RanDF_y_pred))
print('RandomForestRegressor Accuracy:', metrics.r2_score(y_test,RanDF_y_pred))
print('RandomForestRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,RanDF_y_pred)))
RanDF_df = pd.DataFrame({'Actual':y_test, 'Predicted':RanDF_y_pred})
print(RanDF_df)
print("RandomForestRegressor R-squared for Train: %.2f" %RanDF.score(X_train,y_train))
print("RandomForestRegressor R-squared for Test: %.2f" %RanDF.score(X_test,y_test))
RandomForestRegressor 결과값
# random_state=0일때
# RandomForestRegressor Mean Absolute Error: 0.5275022747952686
# RandomForestRegressor Mean Squared Error: 430.61706778889925
# RandomForestRegressor Accuracy: 0.999510651417654
# RandomForestRegressor Root Mean Squared Error: 20.751314844821263
# RandomForestRegressor R-squared for Train: 0.99
# RandomForestRegressor R-squared for Test: 1.00
# random_state=43일때
# RandomForestRegressor Mean Absolute Error: 2.8778434940855315
# RandomForestRegressor Mean Squared Error: 57230.85101455866
# RandomForestRegressor Accuracy: 0.9573706279271497
# RandomForestRegressor Root Mean Squared Error: 239.22970345372806
# RandomForestRegressor R-squared for Train: 1.00
# RandomForestRegressor R-squared for Test: 0.96
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 0.0
27293 1399 1399.0
26497 1599 1599.0
25231 49 49.0
1364 99 99.0
7691 0 0.0
19177 99 99.0
22706 399 399.0
6638 599 599.0
RandomForestRegressor 알고리즘의 Absolute Error 값은 2.8정도였고, Accurary는 0.95였고, 훈련데이터에 의한 알고리즘 정확도는 1이였고, 테스트데이터에 의한 알고리즘 정확도는 0.96이였다.
정확도가 높은 편에 속하는 알고리즘의 알고리즘 전후 가격의 변동은 위처럼 비슷한 결과치를 냈다.
(8) GaussianProcessRegressor
# ------------------------ GaussianProcessRegressor
Gaussian = GaussianProcessRegressor()
# GaussianProcessRegressor 알고리즘 선언
Gaussian.fit(X_train,y_train)
# GaussianProcessRegressor 알고리즘에 나의 데이터를 적용시켜 본다.
Gaussian_y_pred = Gaussian.predict(X_test)
# GaussianProcessRegressor 알고리즘을 사용해서 Y값 예측한다.
print('GaussianProcessRegressor Mean Absolute Error:', metrics.mean_absolute_error(y_test,Gaussian_y_pred))
print('GaussianProcessRegressor Mean Squared Error:', metrics.mean_squared_error(y_test,Gaussian_y_pred))
print('GaussianProcessRegressor Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,Gaussian_y_pred)))
print('GaussianProcessRegressor Accuracy:', metrics.r2_score(y_test,Gaussian_y_pred))
Gaussian_df = pd.DataFrame({'Actual':y_test, 'Predicted':Gaussian_y_pred})
print(Gaussian_df)
print("R-squared for Train: %.2f" %Gaussian.score(X_train,y_train))
print("R-squared for Test: %.2f" %Gaussian.score(X_test,y_test))
GaussianProcessRegressor 결과값
# random_state=0일때
# GaussianProcessRegressor Mean Absolute Error: 465.0475855343884
# GaussianProcessRegressor Mean Squared Error: 1095873.2812232838
# GaussianProcessRegressor Root Mean Squared Error: 1046.839663569968
# GaussianProcessRegressor Accuracy: -0.24533855416145456
# R-squared for Train: 1.00
# R-squared for Test: -0.25
# random_state=43일때
# GaussianProcessRegressor Mean Absolute Error: 469.92498742359925
# GaussianProcessRegressor Mean Squared Error: 1559623.5228000334
# GaussianProcessRegressor Root Mean Squared Error: 1248.848879088272
# GaussianProcessRegressor Accuracy: -0.16171208829481176
# R-squared for Train: 1.00
# R-squared for Test: -0.16
GaussianProcessRegressor 알고리즘은 Absolute Error값은 469였고, Accuracy는 -0.15정도로 낮은 값이였고, 훈련데이터에 의한 제곱근 값은 1이였으나, 테스트데이터에 의한 제곱근 값은 -0.16이였다 이말은 훈련데이터는 잘 맞지만 결과적으로 테스트한 결과값은 좋지 않았다 라는 의미이다.
(9) neutral network.MLPRegressor
# ------------------------ neural_network.MLPRegressor
MLPRe = MLPRegressor()
# MLPRegressor 알고리즘 선언
MLPRe.fit(X_train,y_train)
# MLPRegressor에 나의 데이터를 적용시킨다.
MLPRe_y_pred = MLPRe.predict(X_test)
# MLPRegressor 알고리즘을 통해 Y값을 예측한다.
print('MLPRe Mean Absolute Error:', metrics.mean_absolute_error(y_test,MLPRe_y_pred))
print('MLPRe Mean Squared Error:', metrics.mean_squared_error(y_test,MLPRe_y_pred))
print('MLPRe Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test,MLPRe_y_pred)))
print('MLPRe Accuracy:', metrics.r2_score(y_test,MLPRe_y_pred))
MLPRe_df = pd.DataFrame({'Actual':y_test, 'Predicted':MLPRe_y_pred})
print(MLPRe_df)
print("MLPRe R-squared for Train: %.2f" %MLPRe.score(X_train,y_train))
print("MLPRe R-squared for Test: %.2f" %MLPRe.score(X_test,y_test))
Neutral_network.MLPRegressor 결과값
# random_state=43 일때
# MLPRe Mean Absolute Error: 111.23703423333136
# MLPRe Mean Squared Error: 2185990.942572628
# MLPRe Root Mean Squared Error: 1478.5097032392543
# MLPRe Accuracy: -0.6282725066433816
# MLPRe R-squared for Train: 0.78
# MLPRe R-squared for Test: -0.63
알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격비교
Actual Vs Predict
Actual Predicted
3903 0 -78.006275
27293 1399 1437.266899
26497 1599 1628.240070
25231 49 -59.648284
1364 99 -42.964938
7691 0 -21.436254
신경망 알고리즘인 Neutral_network.MLPRegressor가 좋게 나올줄 알았지만, 나의 데이터에는 맞지 않았다.
예측해서 나오는 값또한 이상했고, Absolute Error 값은 111 이였고, Accuracy는 -0.62였으며 훈련데이터의 제곱근 값은 0.78 테스트데이터의 제곱근 값은 -0.63이였다 .
Part1
수정된 점
1. Scaling부분 : 원래는 데이터전처리 할 때 scaling을 해서 데이터의 정확도를 올려줄려고 하였다. 그러나 scaling을 하게 되면 우리가 가지고 있는 feature와 game_price 값의 변화가 가기 때문에 정확하게 얻지 못할 우려가 있었다. 그래서 scaling은 해놓았지만 하지 않기로 하였다.
2. 데이터전처리를 python에서 진행하려고 했으나, 간단한 전처리는 python보다는 Excel 내내에 하는 것이 훨씬 빨라서 Excel에서 간단한 전처리를 했다.
Part1
최종결과
위의 9가지 알고리즘 중에서 다음 값들을 비교해서 나의 데이터셋에 최적화된 알고리즘을 선별할 수 있었다.
|
Mean Absolute Error: 예측하는 값에 대한 위험도 Accurary : 각 알고리즘에 대한 정확도 R-quared for Train : 훈련데이터에 대한 제곱근 값 R-squared for test : 테스트데이터에 대한 제곱근 값 |
먼저 나의 데이터셋에 정말 맞지 않는 알고리즘들을 제외하면 다음 알고리즘들이 남게된다.
DecisionTreeRegressor,GradientboostingRegressor,BagginRegressor,RandomForestRegressor
이 알고리즘 중에서도 가장 좋은 알고리즘 하나를 선택해야 했다.
그래서 위 4가지 값들을 비교해 보았다.
|
|
DecisionTree |
Gradientboosting |
Baggin |
RandomForest |
|
MAE |
2.47099 |
2.90700 |
2.7680 |
2.8778 |
|
Accurary |
0.967360 |
0.967318 |
0.9609 |
0.9573 |
|
RTrain |
1.00 |
1.00 |
1.00 |
1.00 |
|
RTest |
0.97 |
0.97 |
0.96 |
0.96 |
Accurary à MAE 순으로 비교를 해보았을 때 DecisionTree 알고리즘이 제일 정확하게 나왔다.
MAE도 제일 낮게 나왔으며 테스트데이터의 제곱근 값 또한 1에 가까웠다.
그래서 DecisionTree 알고리즘의 적용전과 후의 가격 예측 비교를 해보았다.
결과값을 보면 다음과 같았다.
Actual Predicted
3903 0 0.0
27293 1399 1399.0
26497 1599 1599.0
25231 49 49.0
1364 99 99.0
7691 0 0.0
19177 99 99.0
22706 399 399.0
6638 599 599.0
7962 99 99.0
14906 99 99.0
20609 299 299.0
21154 299 299.0
8309 199 199.0
12233 1399 1399.0
10926 299 299.0
28605 599 599.0
3131 499 499.0
12642 1999 1999.0
4485 999 999.0
12257 499 499.0
3974 199 199.0
246 0 0.0
11806 99 99.0
12711 799 799.0
3364 0 0.0
21351 199 199.0
23569 0 0.0
4932 999 999.0
15856 149 149.0
4619 299 299.0
26440 1899 1899.0
16355 1499 1499.0
1802 499 499.0
1830 299 299.0
결론을 짓자면, 나의 데이터셋에는 DecisionTreeRegressor가 제일 적합했으며, 오차범위를 정해서 가격의 구분선을 지어야 하지만, 구분선을 짓지 않아도 되었고, 알고리즘 적용 전의 가격과 알고리즘 적용 후의 가격이 거의 일치하는 것을 알 수 있었다.
'학부공부 > 빅데이터기술_프로젝트' 카테고리의 다른 글
| 추가부분 (gradientboostring을 사용해서 예측전후의 편차줄이기) (0) | 2019.05.25 |
|---|---|
| game_price 예측(based on linear regression algorithm) (0) | 2019.05.19 |
| 프로젝트_중간점검(데이터정제과정) (0) | 2019.05.19 |
| 데이터 모으기(4) (0) | 2019.05.05 |
| HTTP Error 403: Forbidden (0) | 2019.05.05 |

#IT #먹방 #전자기기 #일상
#개발 #일상