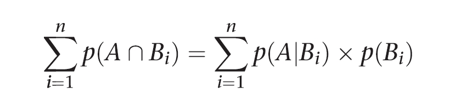베이즈 추론
1. 기반 지식에 있는 모든 규칙을 다음과 같은 형태로 표현한다고 가정을 한다.
è IF : E가 참이다
è THEN : H는 {확률 p로 } 참이다
이 규칙은 사건 E가 발생하고 , 사건 H가 발생할 확률이 p임을 뜻한다.
단순히 A와 B대신 H와 E를 사용한다.
전문가 시스템에서
H는 가설 ( Hypothesis )
E 는 가설을 지지하는 증거 ( Evidence )를 나타낸다.
그렇다면 사건 E가 발생했지만 사건 H가 발생했는지 알지 못한다면 어떨까??
사건 H가 발생할 확률도 계산할 수 있을까??
식으로 나타내면 다음과 같이 나타낼 수 있다.
조금 더 자세히 알아 보자.
--> 식을 풀어서 얘기해 보자면 , 증거 E 가 참일 때 가설 H가 참일 확률을 위 식 처럼 나타 낼 수 있다는 것인데 ,
p(E) 가 분모에 위치하게 될 것이다 . p(E)는 증거 E가 참일 사전 확률을 의미 하는 동시에
` 가설(H)이 참일 때의 증거(E)의 확률 + 가설 (H) 이 거짓일 때의 증거 (E)의 확률 이 두합으로 나타낼 수 있기 때문에 식이 조금 길어보일 뿐이다.
그러면 다음을 어떨까??
단일 증거 E에 기반을 둔 전문가가 단일 가설이 아닌 가설 H1,H2,…Hm을 선택한다면 어떨까 ??
또는 증거 E1,E2,….,Em이 주어지면 전문가도 여러 가설을 만들 수 있을까??
단일 증거 E와 가설 H1,H2,…,Hm에 관한 식 :

증거 E1,E2,….Em 과 가설 H1,H2,…Hm에 관한 식
그렇지만 이것을 적용하려면 , 모든 가설에 대해 모든 증거 조합의 조건부 확률을 알아야 한다 . 이 요건은 전문가에게 엄청난 부담만 주고 , 실제로 작업하기도 어렵다
그러므로 전문가 시스템에서는 증거가 지나치게 세밀해지는 것을 피하고 , 다른 증거 간의 조건부 독립성을 띠게 해야한다 .
실제적으로 값을 구할 수 없는 위 식 대신에 다음 식을 얻을 수 있다.
전문가 시스템은 어떻게 모든 사후 확률을 계산하고 , 잠정적인 참인 가설에 순위를 매길 수 있을까 ??
1. 세 개의 조건부 독립인 증거 E1,E2,E3이 주어지면 전문가는 세 개의 상호 배타적인 총 망라된 가설 H1,H2,H3을 만들고 , 가설에 대한 사전확률 p(H1),p(H2),p(H3)을 제공한다고 가정을 한다
다음 도표는 전문가가 임의의 제공한 값들이다.
먼저 증거3에 대해서 관찰했다고 가정을 하고 다음 식을 도출한다.
이 식을 풀어서 나타내면 다음과 같다
이 값들을 계산해서 보면
0.34
0.34
0.32
차례대로 이렇게 값들이 나오게 되는데 , 증거 E3을 관찰한 후에 가설 H1에 대한 신뢰는 감소한 것을 알 수 있고
H2에 대한신뢰와 같아진 것을 알 수 있다.
반면 H3에 대한 신뢰는 증가한 것을 확인 할 수있다.
아 물론 이 신뢰확인은 전문가가 준 사전확률에 기반한 결론이다.
이렇게 차례대로 증거 2 , 증거 1을 계산해 보면 가설 1과 가설 3만 고려 대상으로 될 것이다.
왜냐하면 가설2는 결과값이 0으로 나오기 때문이다.
'학부공부 > 인공지능' 카테고리의 다른 글
| 베이즈 방법의 치우침 ( bias ) (0) | 2018.09.20 |
|---|---|
| 베이즈 증거 축적을 통한 날씨 분석 (1) | 2018.09.20 |
| 기본 확률 이론 (0) | 2018.09.11 |
| 불확실성 (0) | 2018.09.11 |
| 규칙기반 전문가 시스템의 장점과 단점 (0) | 2018.09.09 |

#IT #먹방 #전자기기 #일상
#개발 #일상