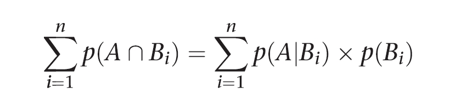

확률의 정의
1. 사건의 확률은 사건이 발생할 경우의 비율이며 , 확률을 가능성에 대한 과학적인 측도로 정의
2. 수학적인 표현으로 1 ( 완전히 확실 ) , 0 ( 완전히 불가능 )
3. 예를 들어서 성공과 실패를 확률로 나타내 보면 다음과 같다
è 성공 = 성공횟수 / 모든 경우의 수
è 실패 = 실패횟수 / 모든 경우의 수
è 성공 = 성공횟수 / 성공횟수 + 실패횟수
è 실패 = 실패횟수 / 성공횟수 + 실패횟수
è 성공 + 실패 = 1
독립 사건과 배타적 사건
1. 동시에 일어날 수 없는 사건
2. 예를 들어서 주사위를 한 번 던질 때 1이랑 4랑 같이 나올 수 있는가 ?? 그럴 수 없다
3. 독립된 사건이 아니면 다른 사건이 발생할 가능성에 영향을 줄 수도 있다.
è 주사위를 한 번 던지는데 , 이번에는 4가 나오지 않는다는 사실을 알고 있을 때 ,5가 나올 확률을 생각해 보면 1/5로 나타낼 수 있다.
조건부확률
1. 사건A가 발생했을 때 , 사건 B가 발생할 확률
2. A를 하나의 사건 , B를 또 다른 하나의 사건이라고 가정을 해보자
3. 사건 A와 B가 상호 배타적이지 않고 , 조건부로써 다른 사건의 발생에 영향을 준다고 가정을 한다.
4. 사건 A가 발생했을 때 사건 B가 발생할 확률을 조건부 확률이라고 한다
5. 조건부 확률은 수학적으로 p(A | B ) 라하고 , 사건 B가 발생했을 때 A가 발생할 확률이라 한다.
6. P(A|B) = A + B ( 각각 발생할 경우의 수 ) / B가 발생할 경우의 수
7. 여기서 A와B가 둘다 발생할 확률을 A와B의 결합 확률이라고 한다
8. 수학적으로 표현하면 p(A n B ) 로 표현한다
è B가 발생하는 비율은 B의 확률인 p(B)
고로 다음 식이 확립된다.
P(A|B) = p(AnB) / p(B)
è P(AnB) = p(A|B) * p(B)
이부분을 조금 더 심화 하면
다음과 같은 식이 성립한다
P(A|B) = p(B|A) x p(A) / p(B)
이 식을 풀어서 나타내면 다음과 같다
P(B|A) = p(BnA) /p(A) 이 되고
전체 식에 p(B|A)을 대입하면
( (P(BnA) / p(A) ) * p(A) ) /p(B)
결국 같은 식이다 .
그런데 이렇게 풀어 놓은 식을 베이즈 규칙이라고 한다.
결합 확률
1. 위에서 소개한 조건부 확률의 개념은 사건 A가 사건 B에 종속되어 있다는 점을 고려했었다.
2. 이 원리를 여러 상호 배타적인 사건들 B1,B2 …Bn에 종속적인 사건 A로 확장할 수 있다
--> 이 식은 조건부 확률을 기반으로 만들어 진 식이다 .
--> 시그마 p(A|Bi)는 Bi가 일어났을 때 A가 일어날 확률인데 , 식으로 나타면
--> p(A n | Bi ) / p( Bi ) 로 나타 낼 수 있는데 , * p(Bi)를 통해서 왼쪽에 나타난 식과 동일하게 나타나는 것을 알 수 있다.
--> 이 식은 방금 위에서 오른쪽에 위치한 식을 풀어놓은 식이다
--> 위 식을 잠깐 보자면 i = 1 부터 n까지 증가하고 , Bi는 i의 값에 따라 n까지 증가한다 . 그러나 증가해도 X p(Bi) 에 의해서
결과적으로 p(A)만 남게 되는 것을 확인 할 수있는데 , 결국 이와 같은 식이 도출되는 것이다.
--> 이 식은 조건부 확률로 p(A)를 표현해 놓은 식이다
--> 시그마 식을 풀어놓으면 분자로 Bi 가 오는데 X p(Bi)에 의해서 분자가 사라지고
--> 분모인 p(A n Bi) 만 남게 된다 . 바로 위에 온 식과 동일하게 생긴것을 확인할 수 있다.
--> 사건 A 가 상호 배타적인 두 사건에만 종속적으로 발생한다면 위와 같은 식이 도출될 수 있다.
--> 식을 풀어서 설명하자면 , B가 발생했을 때의 A사건과 , B가 발생하지 않을 때의 A의 사건 ,
--> 이 두사건의 경우의 수를 더한 것이 p(A)의 값으로 올 수있다는 것이다.
--> 여기서 ㄱ 자 표시는 NOT을 의미한다.
--> p(B) 도 표현할 수 있는데 , A가 발생했을 때의 B의 사건과 , A가 발생하지 않았을 때의 B의 사건
--> 이 두사건의 합을 더한것이 p(B)의 확률이다.
--> 고로 p(A|B)를 베이즈 규칙에 의거해서 베이즈 규칙에 대입을 하면 위와 같은 식이 도출될 수 있다.
--> 풀어서 설명해 보자면 , p(A|B) 는 조건부 확률식으로 바꿔보면 p(AnB) / p(B) 로 나타낼 수 있는데
--> 베이즈 규칙에 의해서 , p(AnB)는 p(B|A) * p(A) 로 바꿔서 표현 할 수있다. 왜냐하면 교환법칙이 성립하기 때문이다.
--> 그러면 분자에는 p(B|A) * p(A) 가 위치하는 것이다.
--> 분모의 결과값을 분석해보자
--> 분모에는 아까 우리가 구한 p(B) 값이 온것인데 , 이것은 상호 배타적인 두 사건이 종속관계일 경우인데
--> A가 발생할 경우와 , A가 발생하지 않을 경우의 B의 확률의 값을 나타낸 것이다.
--> 고로 위와 같은 식이 도출되는 것이다.
--> 이 식은 전문가 시스템에서 불확실성을 다루기 위해 적용하는 확률 이론의 기초가 된다.
'학부공부 > 인공지능' 카테고리의 다른 글
| 베이즈 증거 축적을 통한 날씨 분석 (1) | 2018.09.20 |
|---|---|
| 베이즈 추론 (0) | 2018.09.13 |
| 불확실성 (0) | 2018.09.11 |
| 규칙기반 전문가 시스템의 장점과 단점 (0) | 2018.09.09 |
| 메타지식(metaknowledge) (0) | 2018.09.09 |

#IT #먹방 #전자기기 #일상
#개발 #일상






