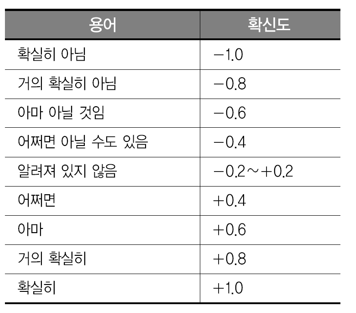
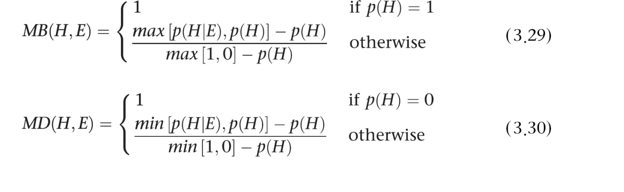베이즈 방법의 치우침 (bias)
1. 베이즈 추론의 주요 입력에는 확률 값이 들어가야 하고 , 이 값을 할당하는 일은 보통 인간의 판단과 관계가 있다.
2. 그러나 심리학 연구에 따르면 인간은 베이즈 규칙과 모순되지 않는 확률 값을 제대로 도출하지 못하고 , 이는 조건부 확률 값이 전문가가 제시한 사전 확률과 모순될 수도 있다는 것을 의미한다.
다음 예제를 보자
시동을 걸었는데도 출발하지 않고 , 이상한 소리를 내는 차가 있다고 가정해보자
차가 이상한 소리를 낼 경우 , 시동 장치가 고장 났을 조건부 확률을 다음과 같이 표현할 수 있음
IF 증상은 ‘이상한 소리’다
THEN 시동 장치가 고장 났다 {확률 0.7}
차가 이상한 소리를 내는데도 시동 장치가 고장 나지 않을 조건부 확률은 다음과 같다
시동 장치가 정상이다 = 1 – 시동 장치가 고장 났다 = 0.3
따라서 다음의 대응 규칙을 얻게 되는 것이다
IF 증상은 ‘이상한 소리’다
THEN 시동 장치가 정상이다 {확률 0.3}
3. 주제 전문가는 조건부 확률을 취급하지 않고 , 대개 숨겨진 내재 확률을 고려 하지 않는다 ( 위에서는 0.3 을 의미 )
4. 베이즈 규칙을 사용하려면 사전 확률 , 즉 차가 출발하지 않을 때 시동 장치가 고장 났을 확률이 필요하다
5. 전문가가 5%의 값을 제공했다고 가정해 보자
6. 다음과 같은 식을 얻을 수 있다.
7. P(시동 장치가 고장 났다 | 이상한 소리) = 이상한 소리날 확률 x 0.05 / 증상은 이상한 소리다 x 0.05 + 증상은 이상한 소리가 아니다 x 0.05
8. 결과값은 0.23 à 이는 전문가의 예측치 0.7보다 낮다
모순이 생기는 이유
1. 모순의 이유는 전문가가 조건부 확률과 사전 확률을 정할 때 다른 가정을 했기 때문인데 사후 확률 p(시동 장치가 고장 났다 | 이상한 소리 ) 에서부터 사전 확률 p(시동 장치가 고장 났다 )까지 거꾸로 생각해 보면 이를 조사할 수 있다.
2. 다음과 같이 가정할 수 있다
3. P(시동 장치가 정상이다 ) = 1 – p(시동 장치가 고장 났다)
4. 베이즈 규칙을 적용하면 다음과 같은 식을 도출할 수있다.
5. P(H) = p(H|E) x p(E|ㄱH) / p(H|E) x p(ExㄱH) + p(E|H)[1-p(H|E)]
6. P(H) = p( 시동 장치가 고장 났다 )
7. P(H|E) = p(시동 장치가 고장 났다 | 이상한 소리 )
8. P(E|H) = p(이상한 소리 | 시동 장치가 고장 났다)
9. P(E|ㄱH) = p(이상한 소리 | 시동 장치가 정상이다 )
è 만일 p(시동 장치가 고장 났다 | 이상한 소리 ) 의 확률을 전문가가 제공한 0.7로 고치면 사전 확률 p(시동 장치가 고장 났다)의 값은 다음과 같이 될 것이다.
è P(H) = 0.7 x 0. 15 / 0.7 x 0.15 + 0.85 x (1 – 0.7 ) = 0.29
이 결과를 보면 전문가가 제시한 5% 보다 거의 6배 정도 큰 값이다 . 이를 통해서 전문가는 사전 확률과 조건부 확률에 대해 매우 다른 추정을 한 것이다
그렇기 때문에 문제를 처리하기 위한 몇 가지 방법이 제안되었다.
è PROSPECTOR
실제 베이즈 접근법을 사용하려면 어떤 가정과 부정 하에서 증거의 조건부 독립을 포함해서 많은 가정을 충족해야 한다
실세계 문제에서는 이런 가정을 제대로 만족하지 못하므로 몇몇 시스템만이 베이즈 추론에 기반을 두고 만들어 졌다.
이 예로 광물 탐사를 수행하는 PROSPECTOR 이 있다.
'학부공부 > 인공지능' 카테고리의 다른 글
| 나머지 10% 의 의미 (0) | 2018.09.20 |
|---|---|
| 확신도 이론과 증거 추론 (0) | 2018.09.20 |
| 베이즈 증거 축적을 통한 날씨 분석 (1) | 2018.09.20 |
| 베이즈 추론 (0) | 2018.09.13 |
| 기본 확률 이론 (0) | 2018.09.11 |

#IT #먹방 #전자기기 #일상
#개발 #일상