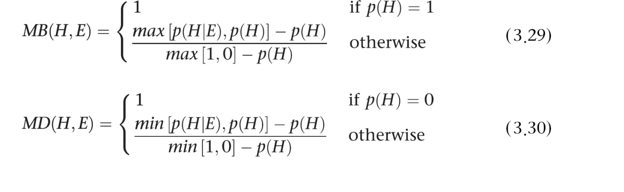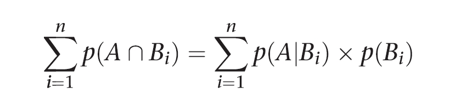베이즈 증거 축적을 통한 날씨 분석을 해볼 것이다.
그러기 위해서는 날씨 분석을 위한 기반지식이 필요하다
다음 그림과 같다 .
# 사용자가 제공한 정보를 바탕으로 전문가 시스템은 내일 비가 올지를 결정한다.
# 강우량이 4.1mm 보다 적으면 강우량이 적은것이고 , 하루 동안의 평균기온이 7.08 보다 이하면 기온이 낮은 것이고
# 높으면 기온이 높다고 가정을 한다
# 일조시간이 하루 4.6시간보다 적으면 흐리다는 것을 의미한다.
먼저 질문을 한다
Q : 오늘의 날씨가 어떻습니까 ??
답변
R : 비가 옵니다.
답변의 결과에 따라서 규칙1이 점화가 되고 풀이 과정은 다음과 같다 .
답변의 결과에 따라서 내일은 비가 온다의 확률과 , 내일은 맑을 확률을 구해볼 수 있는 것이다.
O(H) : 사후 가능성 , 사전 확률을 통해서 구할 수 있다.
O(H | E ) : 사후 가능성 , LS or LN x p(H) 를 통해서 구할 수 있다.
P(H | E ) : 사후 확률인데 , 사후 가능성을 통해 구할 수 있다.
질문자는 다시 물어 본다
Q : 오늘의 강우량은 어떻습니까??
S : 적습니다.
이 질문을 통해서 우리는 규칙3을 점화할 수 있다.
이 때 중요한 점은 사후 가능성을 구할 때 , 위에서 구해 놓은 내일은 맑다의 확률 값을 가져와서 사후 가능성을 구해주는 것
그리고 내일은 맑다의 확률이 0.29 --> 0.80으로 증가한 것을 확인 할 수 있다.
질문자는 다시 물어본다.
Q : 오늘의 기온은 어떻습니까??
S : 낮습니다.
이 질문을 통해서 우리는 규칙4를 점화할 수 있다.
내일은 맑다의 사전 가능성을 구할 때 이전에 구해 놓은 확률을 대입하여서 계산을 해준다.
계산을 통해서 내일은 맑다의 확률이 증가한 것을 확인 할 수 있다.
여기서 중요한 점이 있다.
이 질문을 통해서 규칙5도 점화가 되는데 , AND로 기온이 높다라고 되어있지만
우리는 내일은 비가 온다 라는 가설의 확률을 알고 있으므로 계산이 가능하다.
이 이유는 조건문에서 보았을 때 , LS는 이 조건이 맞다고 생각하는 정도를 수치화한것인데
LN또한 마찬가지이다 . 그렇기 때문에 LN을 통해서 그의 반대의 사전 가능성을 구할 수 있는것
결론을 통해서 내일은 비가온다 라는 확률이 낮아진 것을 확인 가능
질문자는 다시 질문을 한다
Q : 오늘 하늘은 어떻습니까??
S : 흐립니다.
질문의 답을 통해서 규칙 6이 점화가 된다 .
이렇게 규칙 6을 기반으로 질문자의 답변을 통해서 확률을 구해보았다.
결론을 통해서 내일은 맑다 / 내일은 비가 온다 중 --> 내일은 맑다의 가능성이 높다는 것을 의미한다.
'학부공부 > 인공지능' 카테고리의 다른 글
| 확신도 이론과 증거 추론 (0) | 2018.09.20 |
|---|---|
| 베이즈 방법의 치우침 ( bias ) (0) | 2018.09.20 |
| 베이즈 추론 (0) | 2018.09.13 |
| 기본 확률 이론 (0) | 2018.09.11 |
| 불확실성 (0) | 2018.09.11 |

#IT #먹방 #전자기기 #일상
#개발 #일상