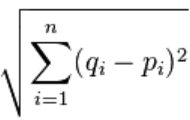

협업필터링 알고리즘 연습2
(Collaborative filtering _ algorithm)
피타고라스 공식을 이용한 유사도도출은 2차원, 즉 비교대상이 2개로 한정되는 한계가 있다.
그렇기 때문에 실제 추천 알고리즘을 구현하고자 하는 데이터에서는 사실상 사용될 일이 없다고 할 수 있다.
다차원에서의 거리를 구해 비교대상이 몇 개로 늘어나든 하나의 함수로 비교할 수 있어야 하고 , 그에 따른 유사도를 구할 수 있어야 한다 .
다차원간 거리를 구하는 데 사용되는 공식들은 다음과 같다.
1. Euclidean distance
2. City-block(Manhattan) distance
3. Minkowski distance
4. Cosine distance
5. Jaccard’s distance
등이 있는데 , 우리가 다뤄 볼 것은 Euclidean distance ( 유클리디안 거리공식 ) 이다.
유클리디안 거리 공식은 무엇인가?
(What is the Euclidian distance formula?)
유클리디안 공식
(Euclidian formula)
식은 위와 같다.
i번째 비교대상 아이템의 값인 (xi-yi)의 제곱을 n번째 까지 모두 구해 더한 다음 제곱근을 취하는 방식이다.
일단 감이 안올수 있기 때문에 , 코드를 통해서 알아보자 .
유클리디안 거리공식을 통한 다차원에서의 두 사람간 거리구하기
(Obtain distance between two people in multi-dimensional through Euclidian distance formula)
여기서는 , 위 공식을 distance(data, name1, name2)로 정의한다.
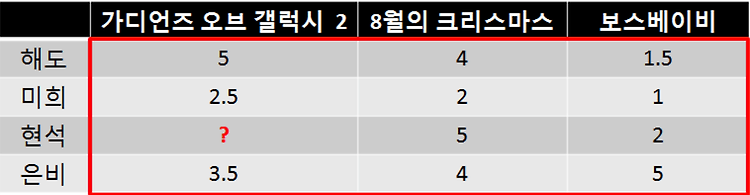
파라미터의 data는 협업필터링1에서 사용한 critics 딕셔너리고 , name1 과 name2 가 비교대상이 될 것이다.
이중 딕셔너리 구조이므로 critics[name] 안에서 for문이 돈다면 딕셔너리 안에 존재하는 value값인 {‘guardians of the galaxy 2’:5,’christmas in august’:4 , ‘boss baby’:1.5} 의 형태로 값이 나오고 , 여기서 다시 key값인 영화 이름을 이용해 평점을 꺼내올 수 있다.
이를 함수로 만들면 아래와 같다 / pow는 제곱을 구하는 메서드
def distance(data, name1, name2):
sum=0
for i in data[name1]:
if i in data[name2]:
sum+=pow(data[name1][i]- data[name2][i],2)
return 1/(1+sqrt(sum))
if i in data[name2]
혹여나 , 같은 영화를 보지 않아 엉뚱한 값이 도출될 수 있으므로 조건문을 통해 같은 영화를 봤을 때만 합을 누적하도록 제한했다.
합을 모두 구했다면 , 피타고라스공식을 사용했을 때와 마찬가지로 정규화를 통해 변수를 일정 범위내로 재설정하고 리턴한다.
위 함수를 사용해 chs 와 leb의 유사도를 구하면 다음과 같다 .
distance(critics,'chs','leb')
è 0.2402530733520421
아이템이 몇 개가 되든지간에 두 사람간 유사도를 구할 수 있게 되었다.
위에서 도출한 distance함수를 통해 전체 데이터에서 거리가 가장 가까운 사람 구하기
이제 두 사람간 유사도를 구할 수 있게 되었다.
한 단계 더 나아가 딕셔너리 전체를 돌며 유사도가 가장 비슷한 사람을 구해본다.
지금은 4명 뿐이지만 , 사람이 몇 명이 되든 적용하도록 새로운 함수를 만들어본다.
코드를 통해서 이해를 해보자 .
li=[] # li는 전역변수로써 점수와 이름을 따로 추출할 때 사용할 것이다 .
def match(data,name,index=3,distance_function=distance):
for i in data:
if name != i: # 자기 자신은 제외
li.append((distance_function(data,name,i),i))
# 유사도 , 이름을 튜플에 묶어 리스트에 추가한다 .
li.reverse() # 내림차순 정렬
return li[:index]
match 라는 함수를 선언해 주게 되는데 , 각 변수들을 알아보자.
data=딕셔너리 ( 영화와 이름 )
name = 기준이 될 사람
index = 몇 위까지 출력할 것인지
distance_function은 위에서 구해 놓은 distance 함수가 된다.
Match 함수가 작동하는 과정은 다음과 같다 .
1. 반복문을 data의 사람수만큼 돌린다.
2. (유사도, 이름)을 튜플로 묶어 빈 리스트에 추가한다 .
출력하면 [(점수,이름),(점수,이름)..] 의 형태가 될 것이다.
3. 마지막으로 보기 쉽게 내림차순 정렬 후 파라미터로 주어진 index 숫자만큼 인덱싱하고 return 한다.
그리고 위에서 정의한 distance 함수에서 같은 영화를 봤을 때 라는 조건이 붙어 있기 때문에 여기서는 자기 자신만 제외하는 조건만 붙이면 된다.
match(critics,'chs')
è [(0.2402530733520421, 'leb'),
è (0.2402530733520421, 'kmh'),
è (0.4721359549995794, 'hhd')]
하나의 함수로 여러 개의 아이템을 비교했고 , chs 와 hhd의 거리가 가장 가까운 것을 확인할 수 있다.
가장 가깝다는 것은 유사도가 높다는 것을 의미한다 .
BARPLOT을 통한 시각화
(Visualization with BARPLOT)
이제 시각화를 위해 bar plot을 사용해볼 것이다 .
그래프를 위해서 matplotlib.pyplot을 import 한 뒤 , 플롯을 그리기 위한 함수 barchart(data, labels)를 정의한다 .
여기서 x축이 유사도가 되고 , y축은 이름이 되는 bar플롯이다.
파라미터의 data는 점수가 들어있는 리스트고 , labels는 이름이 들어있는 리스트가 될 것이다 .
def barchart(data, labels): # data , labels 는 list 형태로 사용
positions = range(len(data))
plt.barh(positions, data, height=0.5,color='r') #가로
plt.yticks(positions, labels)
plt.xlabel('similarity') #x축
plt.ylabel('name') #y축
plt.show #출력
함수를 정의했으니 , 파라미터로 들어갈 data(점수) , label(이름) 를 구해보자
아까 위에서 match()에서 구한 리스트를 확인해 본다 .
[(0.2402530733520421, 'leb'),
(0.2402530733520421, 'kmh'),
(0.4721359549995794, 'hhd')]
여기서 반복문을 통해 이름과 점수를 분리해 한다 .
각 0번째 인덱스를 점수로 , 1번째 인덱스를 이름으로 분리한다.
score = []
names = []
for i in li:
score.append(i[0]) #점수를 담는다.
names.append(i[1]) #이름을 담는다.
점수와 이름을 개별로 리스트 형태로 저장이 잘 되었는지 확인해 보자 .
score
è [0.2402530733520421, 0.2402530733520421, 0.4721359549995794]
names
è ['leb', 'kmh', 'hhd']
barchart(score,names)
è
chs와 유사도 가장높은 사람은 hhd 라는 것을 한눈에 쉽게 알 수 있다.
'졸업작품_preparing.... > python_작업' 카테고리의 다른 글
| Steam_game_ 자동화도구 ( CSV 파일 추가 부분 ) (0) | 2019.02.10 |
|---|---|
| Steam_game_ 검색_자동화도구만들기 (0) | 2019.02.10 |
| Pythons에서 Exel,csv 파일 불러오기 (0) | 2019.01.20 |
| Python_협업필터링_알고리즘3 (0) | 2019.01.01 |
| Python 협업필터링_알고리즘1 (0) | 2018.12.27 |

#IT #먹방 #전자기기 #일상
#개발 #일상