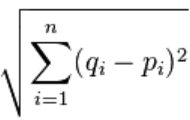

협업필터링 알고리즘 연습3
(Collaborative filtering _ algorithm)
저번에 사용한 유클리디안 거리공식을 활용한 유사도 측정에는 문제점이 있다.
특정인물의 점수기준이 극단적으로 너무 낮거나 높다면 제대로 된 결과를 도출해낼 수 없는 것이다.
예를 들어 나에게 영화를 평가할 때 일정 기준이 있어 , 기대를 충족하지 못하면 모두 0점을 주고 , 아니면 모두 만점을 주면 전체 데이터를 해치는 결과를 낳는다.
이것을 보완한 것이 Correlation_analysis(상관분석)이다.
상관분석은 두 변수간의 선형적 관계에 대한 분석이다.
쉽게 말해서 점수간 관계에 따라 점을 찍은 후 그 점이 분포한 모양에 따라 상관관계를 도출해내는 것이다 .
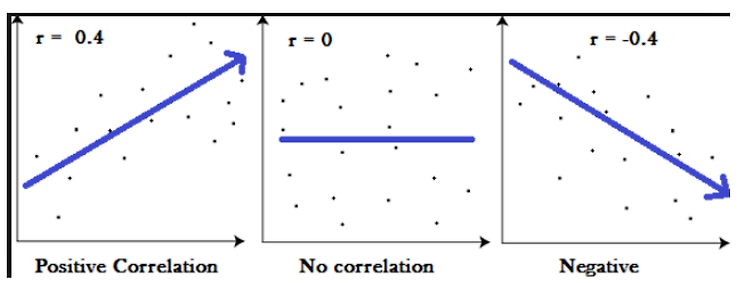
아래 그림과 같이 두 변인 x,y에 대해 x가 변화할 때 y가 변화되면 x,y는 상관관계에 있다고 한다 .
아래에서 r는 기울기를 말한다. 기울기가 양수이면 양의 상관관계라 하며 ,
기울기가 음수이면 음의 상관관계라 한다 .
데이터 정의
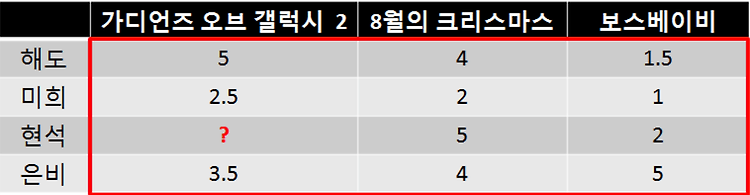
전에 사용했던 예제 딕셔너리 critics를 새로 정의할 것이다 .
조금 더 큰 데이터이며 , 영화의 개수가 많아졌고 , 서로 본 영화의 개수도 다르다.
Critics 는 다음처럼 정의한다 .
critics = {
'김인우': {
'택시운전사': 2.5,
'남한산성': 3.5,
'킹스맨:골든서클': 3.0,
'범죄도시': 3.5,
'아이 캔 스피크': 2.5,
'The Night Listener': 3.0,
},
'김인우1': {
'택시운전사': 1.0,
'남한산성': 4.5,
'킹스맨:골든서클': 0.5,
'범죄도시': 1.5,
'아이 캔 스피크': 4.5,
'The Night Listener': 5.0,
},
'김인우2': {
'택시운전사': 3.0,
'남한산성': 3.5,
'킹스맨:골든서클': 1.5,
'범죄도시': 5.0,
'The Night Listener': 3.0,
'아이 캔 스피크': 3.5,
},
'김인우3': {
'택시운전사': 2.5,
'남한산성': 3.0,
'범죄도시': 3.5,
'The Night Listener': 4.0,
},
'김인우4': {
'남한산성': 3.5,
'킹스맨:골든서클': 3.0,
'The Night Listener': 4.5,
'범죄도시': 4.0,
'아이 캔 스피크': 2.5,
},
'김인우5': {
'택시운전사': 3.0,
'남한산성': 4.0,
'킹스맨:골든서클': 2.0,
'범죄도시': 3.0,
'The Night Listener': 3.5,
'아이 캔 스피크': 2.0,
},
'김인우6': {
'택시운전사': 3.0,
'남한산성': 4.0,
'The Night Listener': 3.0,
'범죄도시': 5.0,
'아이 캔 스피크': 3.5,
},
'김인우7': {'남한산성': 4.5, '아이 캔 스피크': 1.0,
'범죄도시': 4.0},
}
SCATTER PLOT 그려보기
상관분석 전 , 분석에 쓰일 scatter plot을 간단히 그려볼 것이다.
한글 출력을 위해 matplotlib의 font_manager를 import 한다.
from matplotlib import font_manager, rc
font_name = font_manager.FontProperties(fname="C:/Windows/Fonts/HYSUPB.TTF").get_name()
rc('font', family=font_name)
자신이 가져오고 싶은 폰트를 가져오면 된다 .
plt.figure(figsize=(14,8))
plt.plot([1,2,3],[1,2,3],'g^') # 각각의 값과 점의 모양설정
plt.text(1,1,'a') #텍스트 찍기
plt.text(2,2,'b')
plt.text(3,3,'c')
# 각 축의 크기 설정
plt.axis([0,6,0,6])
# 그래프의 x축,y축 크기설정
plt.show()
간단한 사용법을 위해서 (1,1)의 a (2,2)의 b (3,3)의 c 로 그래프에 점을 찍어봤다.
어느 정도 사용법을 익혔다면 이제 critics의 data를 이용해서 scatter plot을 그려보는 함수를 만들 것이다.
함수명은 drawGraph 이다 .
코드를 보면서 확인해 보자 .
import matplotlib.pyplot as plt
def drawGraph(data,name1,name2): # critics data 이용해 scatter plot 그리기
plt.figure(figsize=(14,8)) # plot 크기설정
# plot 좌표를 위한 list 선언
li = []
li2 =[]
for i in critics[name1]: # i = 키 값
if i in data[name2]: # 같은 영화를 평가했을 때만
li.append(critics[name1][i]) # name1의 평점 li[]에 추가
li2.append(critics[name2][i]) # name2의 평점 li2[]에 추가
plt.text(critics[name1][i],critics[name2][i],i) # 영화 제목 text 찍기
plt.plot(li,li2,'ro') # plot그리기
#각 축의 크기 설정 (0~6까지)
plt.axis([0,6,0,6])
# x축과 y축 이름 설정
plt.xlabel(name1)
plt.ylabel(name2)
#그리기
plt.show()
위 함수를 이용해 김인우와 몇 명의 사용자들의 영화평점에 따른 scatter plot을 그려보았다.
drawGraph(critics,'김인우','김인우1')
drawGraph(critics,'김인우','김인우6')
drawGraph(critics,'김인우','김인우7')
6과 7은 1에 비해 좀더 몰려있는 것을 확인할 수 있다 .
두 명간의 상관계수 구하기
위 scatter plot에 따른 상관계수를 구하기 위해 피어슨 상관계수(Pearson Correlation Coefficient) 공식을 이용하겠다. 피어슨 상관계수는 값이 -1부터 1까지 도출되며 , 1에 가까울수록 양의 상관관계이며 , -1에 가까울수록 음의 상관관계를 가진다 .
피어슨 상관계수는 다음의 식을 가진다 .
위 공식에 따라 피어슨 상관계수를 구하는 함수 pearson(data,name1,name2)를 만들어본다.
x값은 name1의 영화 평점이 될 것이고 , y값은 name2의 영화 평점이 될 것이다.
N은 영화 개수가 될 것이고, 같은 영화를 평가했을 때 count라는 변수를 통해 +1 시켜주도록 하겠다.
def pearson(data,name1,name2):
sumX=0
sumY=0
sumPowX=0
sumPowY=0
sumXY=0
count=0
for i in data[name1]: # i = key
if i in data[name2]: # 같은 영화를 평가했을 때만
sumX+=data[name1][i]
sumY+=data[name2][i]
sumPowX+=pow(data[name1][i],2)
sumPowY+=pow(data[name2][i],2)
sumXY+=data[name1][i]*data[name2][i]
count+=1
return ( sumXY- ((sumX*sumY)/count) )/ sqrt( (sumPowX - (pow(sumX,2) / count)) * (sumPowY - (pow(sumY,2)/count)))
위 함수에 실제로 값을 넣어서 , 둘 사이의 상관계수를 구해본다 .
pearson(critics,'김인우','김인우1')
è 0.05477225575051661
pearson(critics,'김인우','김인우6')
è 0.7470178808339965
pearson(critics,'김인우','김인우7')
è 0.9912407071619299
위의 결과값에 따라 서 우리는 다음처럼 생각해 볼 수 있다.
그래프에서 어떠한 결과값들이 겹칠수록 상관계수의 값이 1에 가까워 진다는 것을 알 수 있다 .
전체 인원과의 상관계수 구하기
두 사람간 상관계수를 구하는 함수를 완성했으니 이제 전체 데이터를 돌면서 기준이 될 사람과 나머지 전체간의 상관계수를 한 번에 구해볼 것이다 .
# 딕셔너리 돌면서 상관계수순으로 정렬할 것이다 .
def match(data, name, index=3, function=pearson):
li=[]
for i in data: #딕셔너리를 돌고
if name != i: #자기 자신이 아닐때만
li.append((function(data,name,i),i))
# function을 통해 상관계수를 구하고 li[]에 추가
li.reverse() # 내림차순
return li[:index]
실제로 ‘김인우’와 나머지 인원과의 피어슨 상관계수를 구해보고 , 내림차순으로 6위까지 출력해 본다 .
match(critics,'김인우',6)
è [(0.9912407071619299, '김인우7'), (0.7470178808339965, '김인우6'), (0.5582905262390823, '김인우5'), (0.5669467095138396, '김인우4'), (0.40451991747794525, '김인우3'), (0.39605901719066977, '김인우2')]
우리는 위 함수를 통해서 , 김인우7과 김인우는 거의 유사한 취향을 가졌구나 라고 생각할 수 있다 .
실제 영화 추천하고 , 예상평점 구하기
이제 위에서 구한 함수들을 통해서 실제 영화를 추천하고 예상평점을 구해볼 것이다 .
상관관계는 공동으로 평가를 내린 영화를 기준으로 구한 것이지만 , 영화추천은 아직 대상이 평가를 내리지 않은 영화여야만 한다 .
또한 상관관계가 가장 높은 사람 하나만을 기준으로 영화를 추천하고 예상평점을 구하는 것은 우리가 원하는 바가 아니다 . 유사도의 값을 근거로 하되 , 일정 기준을 충족하는 사람이라면 모두 예상평점과 추천영화를 구하는 데 참고할 수 있다 .
1. 대상을 제외한 모든 사람들의 영화 평점과 유사도를 통해서 추측평점 ((유사도x(타인의)영화평점)을 구한다.
2. 그 추측평점들의 총합을 구한다.
3. 추측평점 총합계 / 유사도 합계 를 통해 모든 사람을 근거로 한 예상평점을 뽑아낼 수 있다.
4. 이 예상평점 값을 보지 않은 영화를 대상으로 모두 구해서 아직 보지 않은 영화중 예상평점이 가장 높은 영화를 추천해주면 될 것이다.
함수명은 getRecommendation()으로 정의할 것이고 함수에 쓰일 데이터 중 위에서 정의한 match()를 통해 함수내 미리 상관계수를 뽑아내는 과정이 필요하다. 결과값은 리스트이고 , 각 데이터는 튜플형태의 ( 예상평점 , 영화제목 ) 형태로 만들 것이다 .
실제로 영화를 추천하는 과정에서 상관관계가 음수라면 고려할 가치가 없다 . 오히려 정확도를 깎을것으로 예상할 수 있기 때문에 조건을 통해 제외해준다 .
코드를 확인해 보자 .
def getRecommendation(data,person,function=pearson):
result = match(critics,person,len(data))
simsum=0 #유사도 합을 위한 변수
score=0 # 평점 합을 위한 변수
li=[] #리턴을 위한 리스트
score_dic={} #유사도 총합을 위한 dic
sim_dic={} #평점 총합을 위한 dic
for sim,name in result: # 튜플이기 때문에 한번에 처리
if sim<0 : continue # 유사도가 양수인 사람만
for movie in data[name]:
if movie not in data[person]: #name이 평가를 내리지 않은 영화
score += sim*data[name][movie] # 그사람의 영화평점 * 유사도
score_dic.setdefault(movie,0) # 기본값 설정
score_dic[movie] +=score # 합계
#조건에 맞는 사람의 유사도의 누적합을 구함
sim_dic.setdefault(movie,0)
sim_dic[movie] += sim
score = 0 # 영화가 바뀌었으니 초기화한다 .
for key in score_dic:
score_dic[key]=score_dic[key]/sim_dic[key] # 평점 총합/ 유사도 총합
li.append((score_dic[key],key)) # list((tuple)) 의 리턴을 위해서
li.sort() #오름차순
#li.reverse() # 내림차순
return li
함수는 완성이 되었고 , 완성된 함수에 데이터와 기준이 될 사람을 넣어 본다 .
getRecommendation(critics, '김인우7')
è [(2.5309807037655645, '킹스맨:골든서클'),
è (2.832549918264162, '택시운전사'),
è (3.4677508474069674, 'The Night Listener')]
기준이 되는 김인우7이 ‘데이터 존재하는 영화 중 보지 않은 영화’는 나이트크롤러 , 택시운전사 , 킹스맨:골든서클이며 , 그는 나이트크롤러에 3.4점을 , 택시운전사에 2.8점을 , 킹스맨:골든서클에 2.5점의 평점을 주리라고 예상할 수 있다 .
여기서 내림차순 정렬을 해주었는데 안되는 이유는 모르겠다. 그래서 오름차순으로 정렬을 해보았다.
일단 결과를 보자면 , 예상평점을 가장 높게 받은 나이트크롤러를 그에게 추천해줄 수 있게 되는 것이다 .
이로써 , 어떠한 추천을 해주는 알고리즘을 배워보았다.
아직은 버겁고 , 어렵다 .
좀더 배워보자 .
'졸업작품_preparing.... > python_작업' 카테고리의 다른 글
| Steam_game_ 자동화도구 ( CSV 파일 추가 부분 ) (0) | 2019.02.10 |
|---|---|
| Steam_game_ 검색_자동화도구만들기 (0) | 2019.02.10 |
| Pythons에서 Exel,csv 파일 불러오기 (0) | 2019.01.20 |
| Python 협업필터링_알고리즘2 (0) | 2018.12.31 |
| Python 협업필터링_알고리즘1 (0) | 2018.12.27 |

#IT #먹방 #전자기기 #일상
#개발 #일상