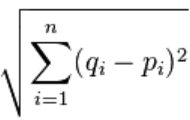

협업필터링 알고리즘 연습1
(Collaborative filtering _ algorithm)
추천 알고리즘을 알고 싶어서 구글링중 괜찮은 사이트가 있어서 따라하면서 배워본다.
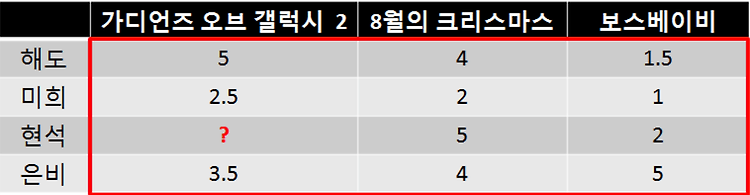
위 처럼 4명의 사람들이 3개의 영화에 대해서 평점을 매겨 놓았다 .
위 Data를 기반으로 협업필터링을 어떻게 구현하게 되는지 맛만 본다.
Key는 이름이고 , Value는 {영화이름 : 평점 } 의 이중 딕션어리 ( Dictionaray ) 구조가 된다 .
critics={
'hhd':{'guardians of the galaxy 2':5,'christmas in august':4,'boss baby':1.5},
'chs':{'christmas in august':5,'boss baby':2},
'kmh':{'guardians of the galaxy 2':2.5,'christmas in august':2,'boss baby':1},
'leb':{'guardians of the galaxy 2':3.5,'christmas in august':4,'boss baby':5}
}
hhd의 키값을 이용해 목록을 구해본다.
파이썬에서 딕셔너리에서 value를 구하는 방법은 [key] or get.(key) 가 있다.
둘 다 value를 뱉어내니 같다고 생각할 수 있겠지만 , 사실상 조금 다르다.
[key] = value를 꺼내올 때 존재하지 않는 키라면 오류가 발생한다.
.get(key) 는 None을 출력한다 .
critics.get('hhd')
-->{'guardians of the galaxy 2': 5, 'christmas in auguest': 4, 'boss baby': 1.5}
hhd 가 boss baby에 몇점을 줬는지 출력해 본다 .
이중 딕셔너리 구조니까 다음과 같이 두 번에 걸쳐 value를 구한다
critics.get('hhd').get('boss baby')
-->1.5
2차원에서 피타고라스 공식을 통해 두 사람간의 거리 구하기
(Finding the distance between two people through the Pythagorean formula in 2D)두 사람 간 유사도를 구하는 가장 기본적인 방법은 2차원 그래프에 점을 찍은 후 서로 거리를 구하는 것이다.
여기에 피타고라스 공식이 사용되며 , 거리가 가까울수록 유사도가 높다고 할 수 있다.
# 피타고라스 공식은 안다고 가정하겠다.
먼저 , 제곱근 계산을 위해 math 패키지의 sqrt를 import 한다.
from math import sqrt
sqrt(pow(1,2)+pow(3,2))
-->3.1622776601683795
위 처럼 값이 잘 나온다 .
이제 위 값을 기반으로 거리공식을 함수로 정의해볼 것이다 .
def sim(i,j):
return sqrt(pow(i,2)+pow(j,2))
위와 같이 정의를 할 수 있다.
이제 두 사람간 거리를 구하는 함수를 만들었으니 , leb와 chs의 boss baby , Christmas in august 평점 거리를 계산해 보자.
var1 = critics['chs']['christmas in august']-critics['leb']['christmas in august']
var2 = critics['chs']['boss baby']-critics['leb']['boss baby']
sim(var1,var2)
위의 공식을 보면 약간 복잡해 보일 수 있는데 , 쉽게 생각하면
Chs의 Christmas in august의 평점에서 leb의 Christmas in august 의 평점을 뺀 값을 var1에 저장시키는 것이다.
그래프로 이해하면 쉬울 것이다.
X 축은 보스베이비 , Y축은 8월의 크리스마스라고 할 때 ,
Chs 의 순서쌍은 ( 2,5 )로 나타날 것이며 ,
Leb 의 순서쌍은 ( 5,4 )로 나타날 것이다 .
결론적으로 ( 5 – 2 )^ + ( 4 – 5 )^ = 결과값^이 된다.
아까 식을 결과값을 내보면
-->3.1622776601683795
이 나온다 .
2차원에서 피타고라스 공식을 통해서 2명 이상과의 거리 구하기
(Finding a distance from two or more people through the Pythagorean formula in 2D)
이제 chs을 대상으로 다른 사람들 전체와의 christmas in august, boss baby 평점을 통해 거리를 구해본다 .
반복문을 통해서 딕셔너리를 돌면서 key값을 순차적으로 꺼내온다 .
그러나 자기 자신을 제외해야 하므로 이를 판별하는 조건문이 중간에 들어갈 것이다 .
for i in critics:
if i!='chs': # 자기자신을 제외시킴
num1 = critics.get('chs').get('christmas in august')- critics.get(i).get('christmas in august')
num2 = critics.get('chs').get('boss baby')- critics.get(i).get('boss baby')
print(i," : ", sim(num1,num2))
-->
hhd : 1.118033988749895kmh : 3.1622776601683795leb : 3.1622776601683795
피타고라스 공식으로 도출한 거리이므로 값이 작을수록 유사한 구조를 가지고 있다.
기준이 되는 chs은 값이 가장 작은 hhd와 가장 유사한 취향을 가졌다고 유추할 수 있게 된다.
비교를 위한 정규화
(Normalization for comparison)
정규화를 이용해 거꾸로 값이 클수록 유사한 것으로 판별하는것으로 한번 해보자 .
정규화를 통하면 변수의 범위가 0~1사이로 일정하게 설정되기 때문에 비교하기 용이하며 , 특정 범위내로 가두는 효과 또한 있다.
for i in critics:
if i != 'chs':
num1 = critics.get('chs').get('christmas in august')- critics.get(i).get('christmas in august')
num2 = critics.get('chs').get('boss baby')- critics.get(i).get('boss baby')
print(i," : ", 1/(1+sim(num1,num2)))
식이 크게 달라지는 것은 없고 , 연산식 나누기가 들어간 것이 보일 것이다 .
-->
hhd : 0.4721359549995794kmh : 0.2402530733520421leb : 0.2402530733520421
위의 결과값을 보면 , 아까와 마찬가지로 chs가 가장 유사한 취향을 가진것으로 동일한 결과를 낸다.
'졸업작품_preparing.... > python_작업' 카테고리의 다른 글
| Steam_game_ 자동화도구 ( CSV 파일 추가 부분 ) (0) | 2019.02.10 |
|---|---|
| Steam_game_ 검색_자동화도구만들기 (0) | 2019.02.10 |
| Pythons에서 Exel,csv 파일 불러오기 (0) | 2019.01.20 |
| Python_협업필터링_알고리즘3 (0) | 2019.01.01 |
| Python 협업필터링_알고리즘2 (0) | 2018.12.31 |

#IT #먹방 #전자기기 #일상
#개발 #일상