
KNeighborsRegressor Analysis학부공부/빅데이터기술2019. 4. 7. 02:08
Table of Contents
반응형
이번에는 KnKNeighborsRegressor Analysis 해볼 것이다.
코드를 통해서 확인해 보자 .
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
from sklearn.model_selection import train_test_split
# from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
--> 먼저 필요한 library를 로딩한다 .
X, y = mglearn.datasets.make_wave(n_samples=40)
# wave 데이터셋을 훈련 세트와 테스트 세트로 나눈다.
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 이웃의 수를 3으로 하여 모델의 객체 생성
reg = KNeighborsRegressor(n_neighbors=3)
# 훈련 데이터를 사용해 모델 학습
reg.fit(X_train, y_train)
print("test prediction:\n{}".format(reg.predict(X_test)))
print("test set R^2:\n{:.2f}".format(reg.score(X_test, y_test)))
score 메소드를 사용해서 , 모델을 평가할 수 있다.
이 메서드는 회귀일 땐 R2값을 반환한다.
결정 계수라고도 하는 R2값은 회귀 모델에서 예측의 적합도를 0과1 사이의 값으로 계산한 것이다.
1은 예측이 완벽한 경우이고 , 0은 훈련 세트의 출력값은 y_train의 평균으로만 예측하는 모델의 경우이다.
결과값은 다음과 같다 .
test prediction:
[-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382
0.35686046 0.91241374 -0.44680446 -1.13881398]
test set R^2:
0.83
KNeighborsRegressor analysis
# 이 1차원 데이터셋에 대해 가능한 모든 특성 값을 만들어 예측해 볼 수 있다.
fig, axes = plt.subplots(1, 3, figsize=(18, 4))
# -3 ~ 3 사이에 1000개의 데이터 생성
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
# 1, 3, 9 이웃을 사용
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
ax.plot(X_test, y_test, '^', c=mglearn.cm2(1), markersize=8)
ax.set_title("{} Neighbor's Training Score: {:.2f}, Test score: {:.2f}".format(
n_neighbors, reg.score(X_train, y_train),
reg.score(X_test, y_test)))
ax.set_xlabel("characteristic")
ax.set_ylabel("target")
axes[0].legend(["model prediction", "training data/target", "test data/target"], loc="best")
plt.show()
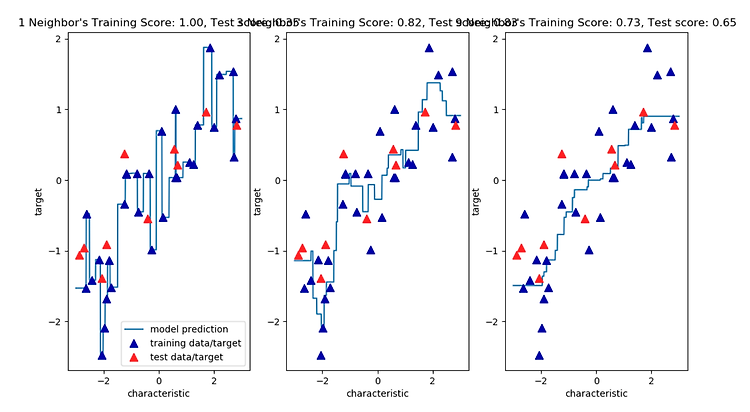
결과값은 다음과 같다.

위 그림에서 볼 수 있듯이 , 이웃을 하나만 사용할 때는 훈련 세트의 각 데이터 포인트가 예측에
주는 영향이 커서 예측값이 훈련 데이터 포인트를 모두 지나간다.
이것은 매우 불안정한 예측을 만들어 낸다.
이웃을 많이 사용하면 훈련 데이터에는 잘 안맞을 수 있지만 더 안정된 예측을 얻게 된다.
반응형
'학부공부 > 빅데이터기술' 카테고리의 다른 글
| 최소제곱법 ( ordinary least squares ) - based on wavedatasets (0) | 2019.04.07 |
|---|---|
| KNeighbors 장단점과 매개변수 (0) | 2019.04.07 |
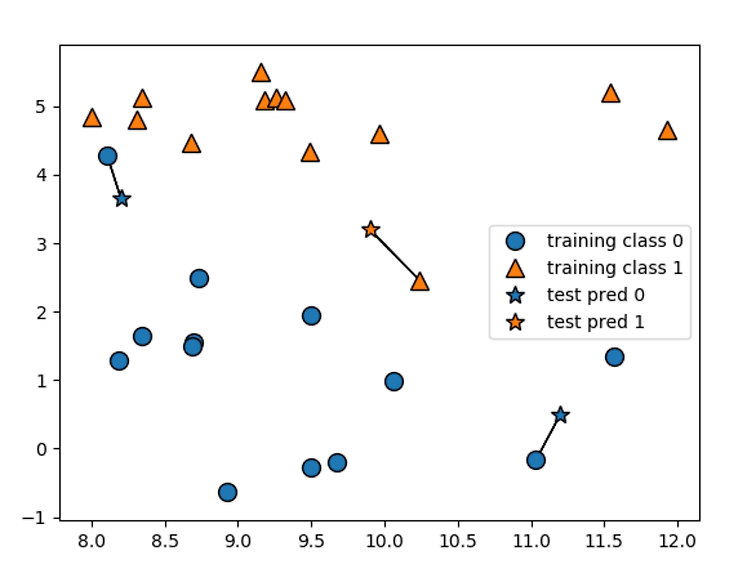
| K-NN 분류기 + KNeighborsClassifier analysis (0) | 2019.04.07 |
| 지도학습..? (0) | 2019.04.02 |
| K-최근접 이웃 분류 (0) | 2019.03.28 |

@IT grow. :: IT grow.
#IT #먹방 #전자기기 #일상
#개발 #일상