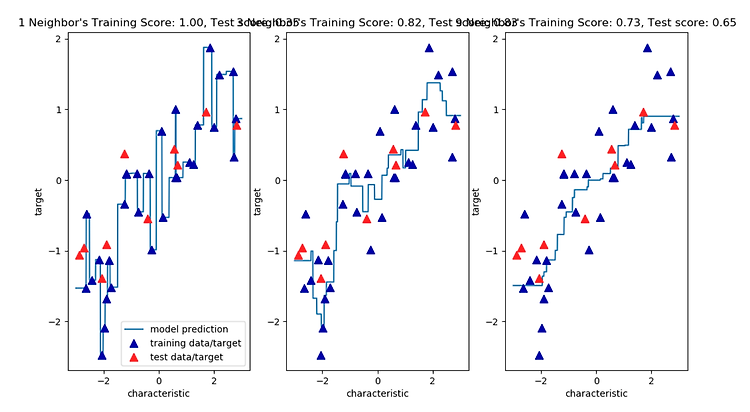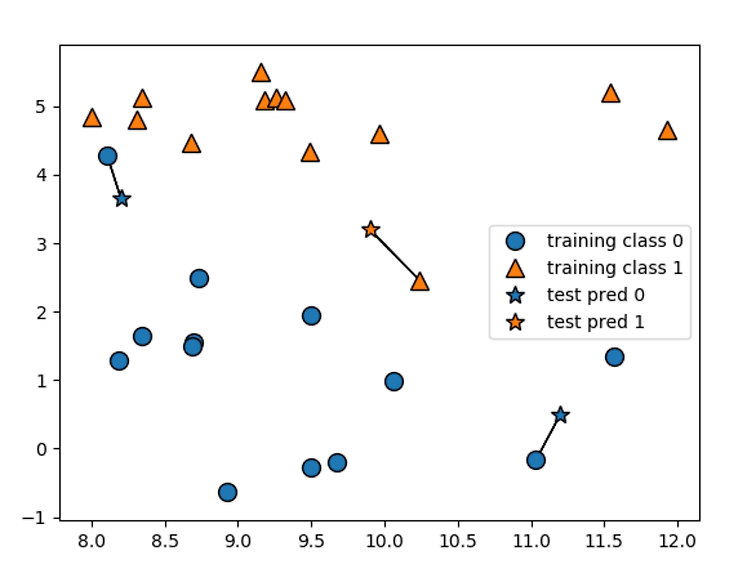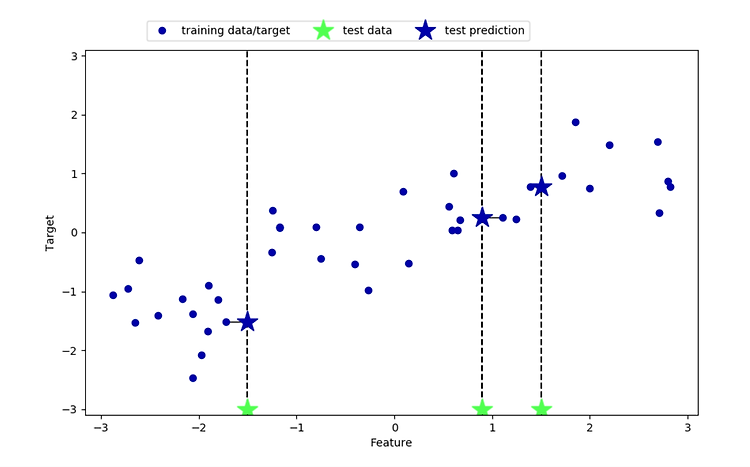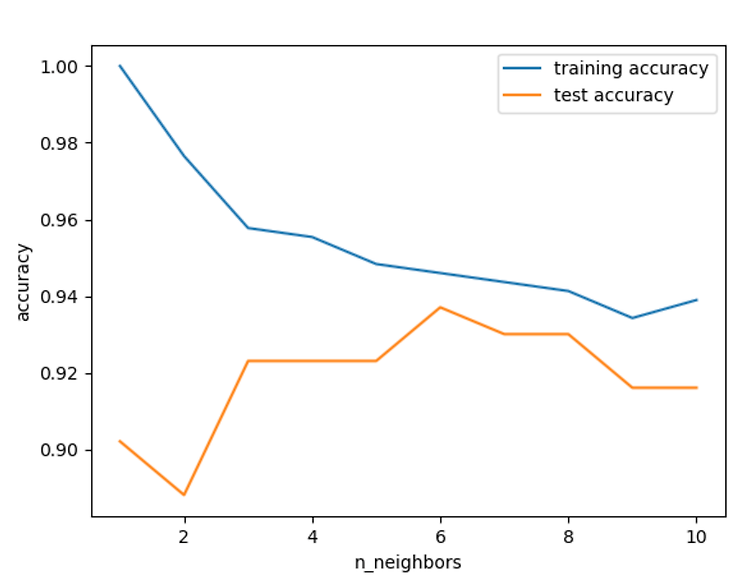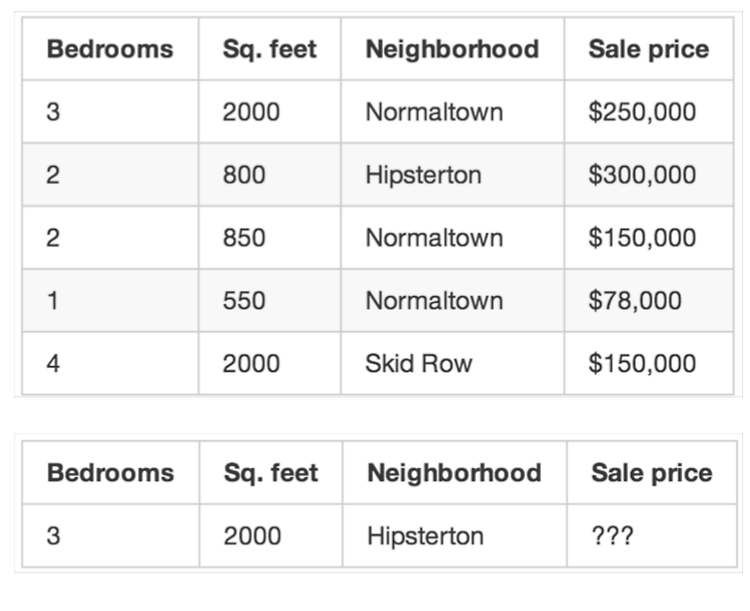


먼저 , 위와 같은 도표가 있다고 하자 .
보면 , 화장실 , 평수 , 위치 , 가격 순서대로 있다는것을 알 수 있다.
그리고 무엇이 생각나는가..?
지도학습은 , 기존의 데이터를 가지고 데이터를 예측해 보는 것인데
화장실 , 평수 , 위치를 기반으로 지도학습을 하여서 회귀를 통한 가격을 예측해 볼 수 있을까?
라는 의문점을 남긴다.
먼저 간단하게 개념정리를 해본다.
매개변수 à y =ax+b à a,b를 찾는 것
è 매개변수를 찾는 것 : 모델링
하이퍼 파라미터 à 일반화 = 최적화 , 사용자가 값을 조정하는 것
è 가중치 : 어떠한 것에 영향을 어느정도 미치는 가에 따라서
è 가중치를 줄 때 , 하이퍼 파라미터를 사용하며 ,
위의 도표를 통해서 , 가격을 예측한다고 했을 때
화장실, 평수, 위치에 따라서 가격이 예측될 것이다 라는 생각을 할 수 있다.
그렇다면 , 각각의 변수에 일정의 비율이 있을 수 있겠다 라는 생각도 할 수 있다.
이 때 , 이 비율을 가중치라고 한다 .
하나의 예를 들어보자 .
자취생이 김치찌개를 해먹으려고 한다.
김치찌개를 먹기 위해서는
일정량의 김치 , 고춧가루 , 참기름 , 두부 , 돼지고기 , 양파 , 대파 , 마늘 등이 들어가는데
정말 맛있는 김치찌개를 만들기 위해서는 이 재료들의 일정량의 비율을 가질 것이다.
위의 도표의 예제또한 마찬가지이다.
완벽한 예측값을 가지기 위해서는 각각의 변수들이 황금비율을 차지했을 때 ,
완벽한 예측을 할 수 있게 되는 것이다.
그렇지만 , 말이 쉽지 그런 일을 쉽지 않다 .
그렇다면 가중치를 찾기 위해서는 어떻게 해야 할까..?
몇 단계로 나누어서 해 볼 수 있다.
1. 각가의 비율(가중치)를 1로 놓고 시작해 본다 .
2.

가중치를 1로 놓았다고 가정하고 , 위같은 결과가 도출되었다면 어떻게 해야할까?
먼저 , 알고있는 모든 주택 데이터를 당신의 함수를 통해 실행해보고 각 주택의
정확한 가격과 이 함수가 얼마나 차이가 나는지 살펴보는 것이다.
위의 예를 보면 , 실제가격은 25만달러이지만 , 추측값은 17만8천달러이다.
차이를 보게되면 8만달러 정도이다.
이제 , 데이터 세트에 있는 각 주택 마다 차이난 가격의 제곱값을 추가해본다.
차이난 가격이라 함은 Sale price - My Guess 의 값을 뺀 값이다.
500개의 주택 판매 정보가 있다고 가정해본다.
위의 처럼 , 차이난 가격의 제곱값을 다 합쳐본다
이 값은 얼마나 잘못되었는지 알 수 있는 값이다.
왜냐면 , 실제가격과 나의 예측값의 차이기 때문이고 ,
이 값이 작을수록 내가 정확하게 예측을 한 것일 것이다.
그리고 이 총합을 500으로 나누면 각 주택별로 얼마나 차이가 나는지 알 수 있다.
이 때 , 평균 오류 값을 이 함수의 비용(cost) 이라 한다.
3. 우리가 가중치를 잘 조정해서 이 비용을 0으로 만들 수 있다면 , 우리의 함수는 완벽해 질 것이다.
다른 가중치를 시도해서 가능한 이 비용을 낮추려는 것이 우리의 목표이자 .
사람들이 예측을 하는 목표이기도 할 것이다.
가능한 모든 가중치를 조합해서 위의 2단계를 계속 반복한다.
이 가중치를 찾게된다면 완벽한 예측을 할 수 있게 될 것이다
여기서 , 2가지의 개념이 나온다.
1. 릿지 ( ridge )
--> 선형 모델 + 가중치 최소화
선형 모델에 가중치를 최소화한 이유는 선형 모델만 사용했을 때는 , 너무 불규칙하기 때문에
가중치를 준 것이다 . 또한 가중치를 크게하면 비용이 커지기 때문이기도 하다 .
2.라쏘 (lasso)
--> 가중치가 0에 가깝다면 , 없애버린다.
즉 , 정리를 해보자면 릿지는 0에 아주 가까운 값이라도 그 특성은 냄겨놓지만 ,
라쏘는 0에 가깝다면 없애버린다 .
0에 가까운것은 없애버리기 때문에 , 특별한 특성만 뽑은 느낌을 주기도 한다 .
'학부공부 > 빅데이터기술' 카테고리의 다른 글
| KNeighborsRegressor Analysis (0) | 2019.04.07 |
|---|---|
| K-NN 분류기 + KNeighborsClassifier analysis (0) | 2019.04.07 |
| K-최근접 이웃 분류 (0) | 2019.03.28 |
| CancetDataset을 이용해서 복잡도와 일반화관계알아보기 (0) | 2019.03.28 |
| Dataset들을 사용해 보자 (0) | 2019.03.28 |

#IT #먹방 #전자기기 #일상
#개발 #일상