다양한 확률분포

다양한 확률분포학부공부/데이터마이닝과통계2018. 11. 24. 17:18@IT grow.

Table of Contents

오늘은 다양한 확률분포에 대해서 다뤄보고자 한다.

정리해 두면 나중에 볼 것 같아서 정리해 본다.

연속형 확률분포에는 다음과 같은 것들이 있다.

1.     정규분포 ( normal distribution ) : norm()
2.     균등분포 ( uniform distribution ) : unif()
3.     지수분포 ( exponential distribution ) : exp()
4.     T – 분포 ( T – distribution ) : t()
5.     F – 분포 ( F – distribution ) : f()
6.     카이제곱분포 ( chisq – distribution ) : chisq()
7.     … 등이 있다.

정규분포는 추정과 검정을 하는 추정통계학 , 회귀분석과 같은 모형 적합시 근간이 되는 확률 분포이다.

우리의 일상 주변에서 흔히 접할 수 있는 확률분포이며 , 중심 극한의 정리에 따라 샘플의 개수 n이 증가하면 이항분포 , 초기하분포 , 포아송분포 등의 이산형 확률분포와 t-분포, f-분포 등의 연속형 확률분포가 정규분포로 근사하게 된다. 따라서 정규분포는 통계에 있어서 정말 중요하고 많이 사용되는 확률분포라고 할 수 있다.

함수 구분		R 함수/ 파라미더
함수 구분		norm()
밀도 함수 (Density function)	d	dnorm(x, mean=0, sd=1)
누적 분포 함수 (Cumulative distribution function)	p	pnorm(q, mean=0, sd=1, lower.tail=TRUE/FALSE)
분위수 함수 (Quantile function)	q	qnorm(p, mean=0, sd=1, lower.tail=TRUE/FALSE)
난수 발생 (Random number generation)	r	rnorm(n, mean=0, sd=1)

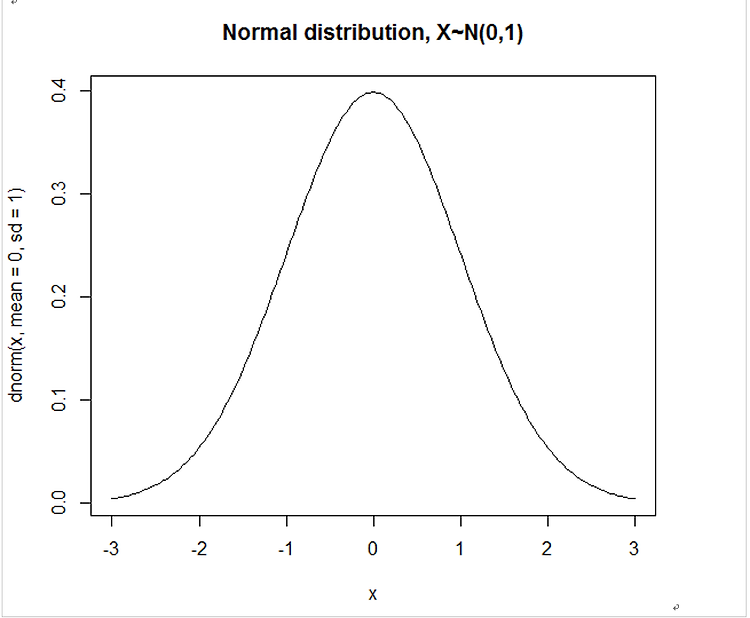
정규분포 그래프 ( normal distribution plot ) : plot(x, dnorm(x))

X <- seq(-3, 3 , length = 200)
Plot(x , dnorm(x, mean=0, sd=1) , type=’1’ , main=”Normal distribution, x~n(0,1)”)

위의 그래프가 정규분포 곡선이다.

X <- seq(-3, 3, length=200)
Plot(x, pnorm(x, mean=0, sd=1), type=’1’, main=”Cumulative normal distribution, x~n(0,1)”)

위의 그래프는 누적 정규분포 곡선이다.

정규분포의 누적분포함수 값 계산 : pnorm()

# p(-1 <= x <= +1)

Pnorm(q=c(1) , mean=0 , sd=1)
Pnorm(q=c(-1), mean=0 , sd=1)
Pnorm(q=c(1), mean=0, sd=1) - Pnorm(q=c(-1), mean=0 , sd=1)

#p(-2 <= x <= +2)

Pnorm(q=c(2) , mean=0 , sd=1)
Pnorm(q=c(-2) , mean=0 , sd=1)
Pnorm(q=c(2) , mean=0 , sd=1) - Pnorm(q=c(-2) , mean=0 , sd=1)

# p ( -3 <= x <= +3 )

Pnorm(q=c(3) , mean=0 , sd=1)
Pnorm(q=c(-3) , mean=0 , sd=1)
Pnorm(q=c(3) , mean=0 , sd=1) - Pnorm(q=c(-3) , mean=0 , sd=1)

# lower.tail = FALSE

Pnorm(q=c(1) , mean=0 , sd=1 ,lower.tail = TRUE)
Pnorm(q=c(1) , mean=0 , sd=1 ,lower.tail = FALSE)

è Pnorm(q,mean,sd,lower.tail=TRUE) 이면 분위수 q를 기준으로 왼쪽의 -inf 부터 q까지의 면적에 대한 합계 값을 보여주며 , pnorm(q, mean,sd,lower.tail = FALSE)이면 분위수 q를 기준으로 q 부터 +inf 까지의 오른쪽으로의 면적 합계 값을 보여주게 된다

분위수 함수 : qnorm(p, mean=0, sd=1 , lower.tail=TRUE/FALSE)

정규분포를 따르는 모집단에서 특정 누적분포함수 값 p에 해당하는 분위수 q를 알고 싶을 때 사용하는 R함수가 분위수 함수 gnorm()이 되겠다.

분위수 함수는 누적분포함수의 역함수이고 , 반대로 누적분포함수는 분위수 함수의 역함수라고 말할 수 있다.

아래를 보면 , 누적분포함수와 분위수 함수가 서로 왜 역함수 인지 알 수 있다.

> # (3) 분위수 함수 : qnorm(p, mean=0, sd=1, lower.tail=TRUE/FALSE)
> pnorm(q=c(1), mean=0, sd=1) # 누적분포함수
[1] 0.8413447

> qnorm(p=0.8413447, mean=0, sd=1, lower.tail = TRUE) # 분위수함수
[1] 0.9999998

> qnorm(pnorm(1))
[1] 1

정규분포 난수 발생 : rnorm()

> # 100s random sampling from normal distribution X~N(0,1)
> random_norm_100 <- rnorm(100, mean=0, sd=1)
> random_norm_100

[1] -0.49990947 1.30162824 -0.55303626 -0.67823807 1.09867201 0.10112825 1.60729584

[8] -0.49131533 -0.23875557 -0.10318560 0.37495367 2.37449966 0.17832867 -1.13884498

[15] -0.04055883 -0.64884566 -0.77738880 -1.07587347 -0.64434199 -1.38282292 0.16584547

[22] 0.44776193 -0.78980486 1.73319388 -0.57968848 1.25727796 -0.05320889 2.61784767

[29] 0.78992548 0.42473023 -1.45674849 1.45782133 2.58232132 -1.85544752 -0.46611618

[36] 0.54686807 -0.72847864 0.12996224 0.19426881 0.01652534 -0.03819245 -0.60196303

[43] -1.33088212 0.33449997 0.08826498 -0.12122490 0.45268734 -0.27621040 0.65957252

[50] 0.73278278 1.23812581 0.09450144 1.44667268 -0.71373007 -0.04135331 1.07079267

[57] 0.85465336 0.10066264 0.07047791 -0.19465235 1.83187324 -0.06047522 -0.89295237

[64] -1.35422679 -0.26235751 1.06455750 0.83675769 -0.16588313 -0.77936548 0.16614752

[71] 0.18333754 0.25274271 1.24194101 -0.36543022 -1.25669837 0.16981720 -0.83342688

[78] 2.58352657 -2.00730559 0.03383145 0.44008506 0.60350848 1.12223002 0.38470856

[85] -1.06631289 -0.08023159 0.28374720 1.68415043 -0.06373142 0.25866477 0.04997717

[92] 0.47737531 -1.07703969 0.25487228 -1.00018975 -0.81282824 -0.77747525 -0.44254534

[99] -0.56190014 0.67733634

> hist(random_norm_100)

난수 발생은 매번 할 때마다 바뀌게 되기 때문에 , 위의 예제를 따라한다면 , 아마 위에 나열된 숫자 , 위에 제시된 히스토그램과는 다른 숫자 , 그래프가 나타날 것입니다.

평균 0을 중심으로 좌우 대칭형태의 정규분포를 띠는 것은 유사할 것이다.

출처: http://rfriend.tistory.com/102 [R, Python 분석과 프로그래밍 (by R Friend)]

T – 분포 ( T – distribution ) : t()

표본분포를 나타낼 때 , T-분포 , F-분포 , 카이제곱 분포 등을 사용한다.

T – 분포는 평균이 0 이며 , 평균을 중심으로 좌우 대칭형태로 되어 있다 .

정규분포보다 가운데의 높이가 조금 낮고 , 좌우의 옆 부분은 정규분포보다 조금 더 높은 형태를 취하고 있다.

T – 분포는 자유가를 모수로 가지고 있으며 , 자유도가 높을수록 , 즉 표본의 개수가 증가할수록 중심극한의 정리에 의해서 정규분포에 근사하게 된다.

표본의 수가 많으면 모집단을 대표할 신뢰도가 높아지게 되어 좋기는 하지만 , 많은 경우는 비용과 시간의 한계로 인해서 한정된 수의 표본만을 추출해서 분석해야 하는 경우가 생기게 된다.

표본의 수가 적은 경우에 표본이 모집단의 어느 한쪽으로 쏠려서 추출될 경우 모집단을 잘 대표할 수 없는 신뢰도 이슈를 보완하기 위해서 , 정규분포일 때보다 평균에서 양쪽으로 멀어지는 바깥쪽 부분의 확률의 수준을 더 높인 분포 T – 분포가 된다.

> install.packages("ggplot2") # install
> library(ggplot2)
> ggplot(data.frame(x=c(-3,3)), aes(x=x)) +
+   stat_function(fun=dnorm, colour="blue", size=1) +
+   stat_function(fun=dt, args=list(df=3), colour="red", size=2) +
+   stat_function(fun=dt, args=list(df=1), colour="yellow", size=3) +
+   annotate("segment", x=1.5, xend=2, y=0.4, yend=0.4, colour="blue", size=1) +
+   annotate("segment", x=1.5, xend=2, y=0.37, yend=0.37, colour="red", size=2) +
+   annotate("segment", x=1.5, xend=2, y=0.34, yend=0.34, colour="yellow", size=3) +
+   annotate("text", x=2.4, y=0.4, label="N(0,1)") +
+   annotate("text", x=2.4, y=0.37, label="t(3)") +
+   annotate("text", x=2.4, y=0.34, label="t(1)") +
+   ggtitle("Normal Distribution, t-distribution")

R에서 T-분포 (t-distribution)을 위해 사용하는 함수 및 Parameter는 아래와 같다.

정규분포는 평균과 표준편차를 parameter로 사용한다.

균등분포는 구간의 최소값과 최대값을 parameter로 사용한다.

지수분포는 Lamda를 parameter로 사용하는데 반해 , T – 분포는 자유도를 parameter로 사용한다

# 자유도는 통계량을 구성하는 확률변수들 중에서 자유롭게 선택가능한 확률변수의 개수를 의미한다.

함수 구분		함수/ Parameter
함수 구분		t()
밀도함수 (density function)	d	dt(x, df)
누적분포함수 (cumulative distribution function)	p	pt(q, df, lower.tail = TRUE/FALSE)
분위수 함수 (quantile function)	q	qt(p, df, lower.tail = TRUE/FALSE)
난수 발생 (random number generation)	r	rt(n, df)

밀도함수 : df(x,df)의 그래프를 정규분포와 비교해서 그려보았으며 , 아래에는 t – 분포의 누적분포 함수를 그래프로 그려보고 누적분포확률도 계산해 본다.

T – 분포 누적분포함수 그래프 : stat_function(fun=pt , args=list(df=1))

> # 누적 t분포 그래프 (Cumulative t-distribution plot) : fun=pt
> ggplot(data.frame(x=c(-3,3)), aes(x=x)) +
+ stat_function(fun=pt, args=list(df=1), colour="brown", size=1.5) +
+ ggtitle("Cumulative t-Distribution : t(1)")

T – 분포 누적분포함수 : pt(q,df,lower.tail= TRUE/FALSE)

위의 t(df=1) 그래프에서 x(-inf,1)범위의 누적분포확률은 0.75 임을 알 수 있다.

> # 누적 t분포 확률 값 계산 : pt(q, df, lower.tail=TRUE/FALSE)
> pt(q=1, df=1, lower.tail = TRUE)
[1] 0.75

T – 분포 분위수 함수 : qt(p, df , lower.tail = TRUE / FALSE )

누적확률분포와 분위수 함수는 역의 관계에 있는데 , 위의 pt(q=1, df=1 , lower.tail=T) = 0.75였으므로 누적확률분포값이 0.75 가 되는 분위수 q는 ‘1’이 되는지 아래 R script로 확인해 보겠다.

> # t분포 분위수 함수 값 계산 : qt(p, df, lower.tail=TRUE/FALSE)
> qt(p=0.75, df=1, lower.tail = TRUE)
[1] 1

T – 분포 난수 발생 : rt(n,dt)

T 분포에서 rt(n,df) 함수를 이용해서 난수를 발생시켜보겠다. 난수는 매번 생성할 때마다 바뀌므로 매 시행마다 아래의 예제와는 조금씩 달라지게 된다.

평균 0을 중심으로 좌우 대칭형태를 띌 것이다.

> rt <- rt(50, df=1)
> rt
[1] -1.89734826 -1.40787172 -2.38022561 -0.21218535 0.71259957 -0.37759519 -0.46671360 -0.20455553
[9] -0.54603347 2.88325761 0.13593286 0.09719242 1.35843796 -1.86861627 5.69879846 1.23054665
[17] -1.24953468 -0.76327864 1.87092396 -0.39719483 -0.42141574 0.10862682 0.54106231 0.30827837
[25] -1.25508149 0.54352324 -1.92825750 0.22491497 -0.63797793 -0.37089263 7.31876302 2.25023970
[33] -1.60455685 -1.64779189 -5.54583982 -8.82959795 0.53445244 -0.47451960 -2.52582931 1.57372391
[41] 2.30557669 -0.04118914 -0.71146732 -0.27621122 -7.29220086 -0.52472800 -0.78465027 -2.07649916
[49] 0.38322764 -1.71782797
>
> hist(rt, breaks=20)

출처: http://rfriend.tistory.com/110 [R, Python 분석과 프로그래밍 (by R Friend)]

R 균등분포 ( uniform distribution ) : Unif()

균등분포는 연속형 확률 분포 중에서 가장 간단한 형태로서 , 구간 [mi=a,max=b]에서 값이 균등하게 퍼져 있는 집단 , 일어날 확률이 균등한 분포를 말한다.

예를 들자면 , 김포공항에서 제주도 공항까지 비행기로 이륙에서 착륙까지 걸리는 총 비행시간이 1시간~1시간5분 사이라고 하면 , 0~59분59초까지는 비행기가 도착할 확률이 0 ,

1시간 ~1시간5분 사이에 도착할 확률은 1, 1시간 5분 이후는 다시 확률이 0이 되는 균등분포를 따른다고 할 수 있다.

R 에서 사용하는 균등분포 함수 및 파라미터들은 아래와 같으며 , 필요한 함수 , 파라미터를 가져다 사용하면 되겠다.

함수 구분		균등분포 함수/파라미더
함수 구분		unif()
밀도함수 (density function)	d	dunif(x, min, max)
누적분포함수 (cumulative distribution function)	p	punif(q, min, max, lower.tail=TRUE/FALSE)
분위수 함수 (quantile function)	q	qunif(p, min, max, lower.tail=TRUE/FALSE)
난수 발생 (random number generation)	r	runif(n, min, max)

균등분포 그래프 : fun = dunif

Ggplot2 의 fun = dunif() 함수를 사용해서 균등분포를 그래프로 그려보면 아래와 같이 특정 구간 [a , b] 에서 확률이 균등함을 알 수 있다.

> library(ggplot2)
> # uniform distribution plot (min=0, max=10)
> # 균등분포 : fun = dunif
> ggplot(data.frame(x=c(-2,20)), aes(x=x)) +
+ stat_function(fun=dunif, args=list(min = 0, max = 10), colour="black", size=1) +
+ ggtitle("Uniform Distribution of (min=1, max=10)")

누적 균등분포 그래프 : fun = punif

누적 균등분포 그래프를 그려보면 아래와 같다.

> # (2) 누적균등분포 함수 그래프 (Cumulative Uniform distribution plot) : fun = punif
> ggplot(data.frame(x=c(-2,20)), aes(x=x)) +
+ stat_function(fun=punif, args=list(min = 0, max = 10), colour="black", size=1) +
+ ggtitle("Cumulative Uniform Distribution of (min=0, max=10)")

누적 균등분포 함수의 확률 값 계산 : punif()

> # (3) 누적 균등분포함수(cumulative uniform distribution function) 확률 값 계산 : punif()
> # : punif(q, min, max, lower.tail = TRUE/FALSE)
> punif(3, min=0, max=10, lower.tail=TRUE)
[1] 0.3

> # Uniform Distribution of (min=1, max=10), x from 0 to 3"
> ggplot(data.frame(x=c(-2,20)), aes(x=x)) +
+   stat_function(fun=dunif, args=list(min = 0, max = 10), colour="black", size=1) +
+   annotate("rect", xmin=0, xmax=3, ymin=0, ymax=0.1, alpha=0.2, fill="yellow") +
+   ggtitle("Uniform Distribution of (min=1, max=10), x from 0 to 3")

균등분포 분위수 함수 값 계산 : qunif(p, min , max , lower.tail= TRUE/FALSE)

이전 정규분포와 함수는 qunif()로 동일하지만 , 괄호 안의 parameter 들은 다르다.

> # (4) 분위수 함수 : qunif(p, min, max, lower.tail=TRUE/FALSE)
> qunif(0.3, min=0, max=10, lower.tail = TRUE)
[1] 3

난수 발생 : runif(n, min, max)

난수는 매번 실행할 때마다 바뀌므로 제가 아래에 제시한 것과는 다른 숫자 , 다른 그래프가 그려질 것이지만 , 형태는 균등분포를 띠는 유사한 모양이 될 것이다.

> ru_100 <- runif(n=100, min=0, max = 10)
> ru_100

[1] 7.33957568 2.78596723 6.30797744 5.01438337 6.57949706 5.90883342 3.51446293 9.28736811

[9] 9.55213668 5.59377524 4.71003185 3.29525512 0.25759555 9.40326151 6.56466466 2.44973803

[17] 4.88714900 3.10710648 3.84375758 8.55017741 3.09487276 0.13411621 0.44285713 8.90632265

[25] 0.07968823 5.03465390 4.64601169 1.23565062 4.81310463 1.59225023 7.03799510 0.68870704

[33] 4.03014086 9.97756283 5.55815726 2.01819345 7.00497545 8.50399118 2.29608430 2.92359120

[41] 0.85656712 6.52544881 6.37193951 6.15247601 5.29502105 7.68988134 6.37691223 0.37387705

[49] 6.89023959 1.65049129 3.75195268 7.97220092 6.50160025 9.52491436 1.70569894 9.80475205

[57] 0.24770673 8.47412000 4.66718922 2.52269224 2.81985175 8.79845402 6.03852213 8.10848875

[65] 1.10510449 9.35548906 1.83535387 0.47889795 6.54578585 1.61742080 4.51840400 3.99912651

[73] 4.82545376 4.04589108 0.71750065 7.56085867 1.22887762 2.97822070 5.14541682 3.59126885

[81] 5.00911758 1.02152702 7.78324707 4.69437196 1.13090493 3.70933500 0.03173870 5.74159309

[89] 2.68879279 3.36398725 9.34593590 6.18818473 9.43490689 5.82578697 4.49576854 2.90029081

[97] 3.34726356 7.19013351 9.97276521 9.39421932

> # density plot of runif(n=100, min=0, max = 10) & adding line of 0.1 uniform probability
> hist(ru_100, freq=FALSE, breaks=10, col="yellow")
> abline(h=0.1, lty=3, lwd=3, col="red")

출처: http://rfriend.tistory.com/106 [R, Python 분석과 프로그래밍 (by R Friend)]

지수분포 (exponential distribution) : exp()

지수분포는 어떤 특정 사건이 발생하기 전까지 걸리는 시간을 나타내기 위해 많이 사용되는 확률분포이다.

지수분포의 예로는 전자레인지의 수명시간 , 콜센터에 전화가 걸려 올 때까지 걸리는 시간 , 경부고속도로 안성나들목에서 다음번 교통사고가 발생할 때까지 걸리는 시간 , 은행 지점에 고객이 내방하는데 걸리는 시간 등이 있겠다.

이산형 확률분포 중에서 포아송 분포가 단위 시간 혹은 단위공간에서 특정 사건이 발생하는 횟수에 대한 분포를 나타낼 때 주로 사용한다고 했는데 , 헷갈리지 않도록 주의를 해야겠다.

확률변수 X의 확률밀도함수가 위와 같을 때 , 확률변수 X는 모수 λ 인 지수분포를 따른다고 말한다.

R에서 지수분포와 관련된 함수 및 파라미터는 다음과 같다.

함수 구분		지수분포 함수/파라미터
함수 구분		exp()
밀도 함수 (Density function)	d	dexp(x, rate)
누적분포 함수 (Cumulative distribution function)	p	pexp(q, rate, lower.tail=TRUE/FALSE)
분위수 함수 (Quantile function)	q	qexp(p, rate, lower.tail=TRUE/FALSE)
난수 생성 (Random number generation)	r	rexp(n, rate)

지수분포 그래프 : fun = dexp

> library(ggplot2)
> # (1) 지수분포 그래프 (Exponential distribution plot) : fun=dexp
> ggplot(data.frame(x=c(0,10)), aes(x=x)) +
+   stat_function(fun=dexp, args=list(rate=1), colour="brown", size=1.5) +
+   ggtitle("Exponential Distribution")
>     +   ggtitle("Exponential Distribution")

누적 지수분포 그래프 : fun = pexp

> # (2) (Cumulative exponential distribution plot) : fun=pexp
> ggplot(data.frame(x=c(0,10)), aes(x=x)) +
+ stat_function(fun=pexp, args=list(rate=1), colour="brown", size=1.5) +
+ ggtitle("Cumulative Exponential Distribution")

누적 지수분포 확률 값 계산 : pexp(q, rate , lower.tail = TRUE/FALSE)

> pexp(q=2, rate=1, lower.tail = TRUE)
[1] 0.8646647

λ (rate) = 1 인 지수분포에서 0~1까지의 누적 확률 값은 0.8646647 임을 알 수 있다.

지수분포 분위수 함수 값 계산 : qexp(p, rate , lower.tail=TRUE/FALSE)

> qexp(p=0.8646647, rate=1, lower.tail = TRUE)
[1] 2

qexp()는 pexp()와 역의 관계에 있다고 보면 되겠다.

지수분포 난수 발생 : rexp(n, rate)

> rexp(100, rate=1)

[1] 0.805385854 1.077017598 0.941678341 2.059229603 0.517943248 0.955476408 0.575837716

[8] 0.851462637 0.086982322 1.243358626 1.077268675 2.604957888 0.007571515 1.793674221

[15] 0.118729103 0.096055712 0.015758928 0.201158101 0.914114063 0.130984491 2.752139235

[22] 0.829986667 0.651976457 1.265562156 2.635988993 1.190808342 0.444055191 1.480476206

[29] 1.741018226 2.692880185 0.804053361 3.127147071 0.902618388 1.432761851 0.369694262

[36] 0.290926187 0.576759913 0.827636680 1.634353038 2.113214617 0.570110160 0.609782309

[43] 1.985241502 1.067016441 0.098556668 3.326005637 2.261946740 6.395236475 1.906314444

[50] 0.503994692 1.578938061 0.144050682 0.361734510 1.495605791 1.167056286 1.397221429

[57] 1.598533234 0.370363955 0.153343928 0.351399011 0.957647500 1.053767695 0.272256882

[64] 1.176451771 0.222995248 1.125289913 0.076051627 3.489328747 0.199440748 3.143880822

[71] 1.640546855 4.492400575 1.102261695 0.189814932 0.222941682 2.305212835 0.069710370

[78] 1.972949872 0.201703040 1.783014953 1.297271054 2.173743544 2.350792197 2.018307233

[85] 0.417343667 2.533255698 0.522270208 2.068958899 1.062778262 0.210765630 0.804149691

[92] 1.261281259 0.006859250 0.620238345 3.478939042 2.692230696 0.557543887 1.830330845

[99] 0.478452368 0.904496278

> hist(rexp(100, rate=1), breaks=10)

Dexp(x, rate , log=TRUE)

Log = TRUE 옵션을 설정하면 지수분포의 확률밀도함수값에 밑이 e (약 2.17)인 자연로그 In을 취한 값을 계산한다 .

아래에는 X 가 모수가 1인 지수분포를 따른다고 했을 때 , x : 1 , 2 , …. 10 의 확률밀도함수값을 계산한 것이다.

Log = TRUE 라는 옵션을 취한값과 , log(dexp)라는 수식을 직접 입력해서 계산한 값이 서로 정확히 일치함을 알 수 있다.

> # dexp(x, rate, log=TRUE)
> dexp <- dexp(c(1:10), rate=1)
> dexp_log <- dexp(c(1:10), rate=1, log=TRUE)
>
> exp_df <- data.frame(cbind(c(1:10), dexp, dexp_log))
> exp_df
   V1         dexp dexp_log
1   1 3.678794e-01       -1
2   2 1.353353e-01       -2
3   3 4.978707e-02       -3
4   4 1.831564e-02       -4
5   5 6.737947e-03       -5
6   6 2.478752e-03       -6
7   7 9.118820e-04       -7
8   8 3.354626e-04       -8
9   9 1.234098e-04       -9
10 10 4.539993e-05      -10
>
> exp_df <- transform(exp_df, dexp_logarithm = log(dexp))
> exp_df
   V1         dexp dexp_log dexp_logarithm
1   1 3.678794e-01       -1             -1
2   2 1.353353e-01       -2             -2
3   3 4.978707e-02       -3             -3
4   4 1.831564e-02       -4             -4
5   5 6.737947e-03       -5             -5
6   6 2.478752e-03       -6             -6
7   7 9.118820e-04       -7             -7
8   8 3.354626e-04       -8             -8
9   9 1.234098e-04       -9             -9
10 10 4.539993e-05      -10            -10

디폴트인 dexp(x , log=FLASE) 와 dexp( x, log=TRUE) 옵션 설정해서 나온 값을 가지고 그래프로 그려서 비교해보면 아래와 같다 . log = TRUE 설정을 해서 자연로그를 취했더니 , 원래 밑으로 축 쳐졌던 지수분포 그래프가 곧은 직선으로 변환되었음을 알 수 있다.

> my_par = par(no.readonly = TRUE)
> par(oma = c(0, 0, 1, 0))
> par(mfrow = c(1, 2))
>
> plot(dexp, main = "dexp : log = F")
> plot(dexp_log, main = "dexp : log = T")
>
> mtext("density function of exponential distributin : log = FALSE vs. log = TRUE",
outer = TRUE, cex = 1.2)

출처: http://rfriend.tistory.com/107 [R, Python 분석과 프로그래밍 (by R Friend)]

포아송 분포 ( Poisson distribution ) : pois()

이산형 확률 분포에는

1.     이항분포 ( Binomial distribution ) : binom()
2.     초기하분포 ( Hypergeom etric distribution ) : hyper()
3.     포아송 분포 ( Poisson distribution ) : pois()
4.     …. 등이 있다 .

확률변수 x 가 이항분포 B(n,p)를 따를 때 , np = λ 로 일정하게 두고 , n이 충분히 크고 p가 0에 가까울 때 이항분포에 근사하는 포아송 분포는 아래와 같다 .

포아송 분포는 일정한 단위 시간 , 단위 공간에서 어떤 사건이 랜덤하게 발생하는 경우에 사용할 수 있는 이산형 확률분포이다.

예를 들어서 1시간 동안 은행에 방문하는 고객의 수 , 1시간 동안 콜센터로 걸려오는 전화의 수 , 1달 동안 경부고속도로에서 교통사고가 발생하는 거수 , 1년 동안 비행기가 사고가 발생하는 건수 등이 있다.

포아송 분포에서 모수 λ (lambda 라고 발음함) 는 일정한 단위 시간 또는 단위 공간에서 랜덤하게 발생하는 사건의 평균 횟수를 의미한다.

함수 구분		포아송 분포 R 함수/ 모수 pois()
밀도 함수	d	dpois(x, lambda)
누적 분포 함수	p	ppois(q, lambda, lower.tail = TRUE/FALSE
분위수 함수	q	qpois(p, lambda, lower.tail = TRUE/FALSE
난수 발생	r	rpois(n, lambda)

λ = 3 인 포아송 분포 그래프 (Poisson distribution plot of lambda = 3)

> # (1) 포아송 분포 그래프 (Poisson distribution plot)
> plot(dpois(x=c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10), lambda = 3),
+ type='h',
+ main = "Poisson distribution, lambda = 3")

P ( X = 15 ) 확률 계산 : dpois ( x , lambda )

예를 들어서 , 어느 은행의 1시간당 방문 고객 수가 λ = 20 인 포아송 분포를 따른다고 한다 .

그렇다면 1시간당 방문고객수가 15명일 확률은?

> # (2) P(X = 15) in Poisson distribution with lambda = 20
> dpois(x=15, lambda = 20)
[1] 0.05164885

P( x <= 15 ) 확률 계산 : ppois ( q , lambda , lower.tail = TRUE )

어느 은행의 1시간 당 방문 고객 수가 λ = 20 인 포아송 분포를 따른다고 할 때 , 1시간당 방문고객수가 15명 이하일 확률은??

> # (3) P(X =< 15) in Poisson distribution with lambda = 20
> ppois(q=15, lambda = 20, lower.tail = TRUE)
[1] 0.1565131

> sum(dpois(x=c(0:15), lambda = 20)) # the same result with the ppois()
[1] 0.1565131

특정 확률 값에 해당하는 분위수 계산 : gpois( p, lambda , lower.tail = TRUE )

어느 은행의 1시간 당 방문 고객 수가 λ = 20 인 포아송 분포를 따른다고 한다.

만약 1시간 동안 방문한 고객수에 해당하는 확률이 15.65131% 라면 이는 몇 명에 해당하는 가 ?

> qpois(p=0.1565131, lambda = 20, lower.tail = TRUE)
[1] 15

난수 발생 : rpois ( n , lambda )

λ = 20 인 포아송 분포에서 n = 1000 개의 난수를 발생시키고, 도수분포표를 구하고, 도수별 막대그래프를 그려보아라.

> rpois(n=1000, lambda = 20)
[1] 18 17 21 16 19 25 18 22 18 24 28 23 21 11 19 25 20 27 24 27 12 17 11 16 17 18 21 17 16 22 16
[32] 20 24 18 26 15 20 17 25 18 16 23 18 17 20 28 18 16 21 18 21 20 16 21 22 11 20 18 20 10 15 17
[63] 14 15 22 20 16 26 18 25 14 11 22 24 23 19 26 12 17 23 17 24 21 17 19 24 28 26 18 24 17 19 18
[94] 19 24 22 23 20 25 21 22 16 20 24 20 22 24 25 22 23 20 19 28 19 21 15 27 27 17 14 20 25 26 25
[125] 26 16 22 16 22 21 15 15 21 19 29 15 23 21 23 31 16 33 18 21 24 28 34 25 19 24 22 23 30 27 21
[156] 20 16 18 18 13 21 20 23 21 15 12 18 25 16 15 26 18 22 18 10 26 23 19 13 18 22 23 21 22 12 20
[187] 20 19 17 18 18 15 20 11 25 21 20 20 20 22 19 31 18 23 16 18 21 29 19 20 20 16 22 18 16 22 18
[218] 14 18 23 18 22 15 15 14 19 20 23 11 20 17 21 23 17 21 12 28 22 19 16 20 14 27 20 26 19 22 19
[249] 22 21 20 24 21 23 25 14 19 18 22 8 20 13 19 22 22 20 18 15 22 22 13 20 24 18 25 18 19 30 22
[280] 18 30 22 10 25 21 18 19 19 7 25 15 27 23 26 21 16 21 19 21 24 16 18 18 21 25 10 15 25 18 21
[311] 18 27 15 26 21 33 13 20 18 22 27 16 11 18 18 26 20 28 20 17 22 19 24 25 13 13 16 21 21 21 20
[342] 18 21 18 16 11 15 24 19 24 31 23 24 17 21 20 19 16 20 23 27 18 23 20 14 27 14 26 15 14 10 23
[373] 22 29 20 17 24 29 26 17 15 16 23 27 14 17 21 21 14 22 27 16 22 19 19 15 25 20 23 16 20 16 16
[404] 20 18 18 16 31 15 13 15 16 18 17 23 19 20 18 24 13 24 20 25 22 15 17 25 12 11 19 16 19 26 29
[435] 23 18 17 15 23 18 32 23 30 21 19 24 24 21 17 22 23 27 21 23 17 20 20 22 15 15 21 32 23 24 16
[466] 28 18 23 24 22 20 18 19 18 15 16 16 20 17 16 12 18 25 23 21 17 19 21 24 20 16 20 26 19 21 28
[497] 25 16 14 19 16 19 25 9 12 20 20 18 23 27 19 12 9 21 15 27 17 21 23 18 17 11 23 20 19 25 18
[528] 17 19 22 18 28 25 25 17 26 30 26 17 22 16 22 16 31 15 25 16 23 15 23 15 20 20 18 21 19 15 23
[559] 24 23 21 21 14 15 20 23 29 19 15 18 18 12 19 17 22 33 24 19 10 26 22 24 23 25 14 16 19 18 21
[590] 19 32 18 20 22 23 16 18 22 16 25 14 19 23 19 14 17 24 26 19 18 27 20 21 19 21 27 20 30 17 26
[621] 23 27 23 23 24 26 21 21 13 21 20 22 16 23 22 27 16 22 25 26 14 32 27 34 19 18 23 19 19 17 15
[652] 29 15 19 18 16 19 19 15 16 19 28 18 19 17 14 19 23 25 31 24 24 14 19 17 19 25 20 24 21 17 20
[683] 20 25 24 18 16 22 20 18 16 22 17 12 20 25 21 39 22 19 12 12 25 18 31 23 15 20 20 23 15 23 15
[714] 22 17 14 14 13 16 17 22 18 14 26 28 21 17 24 26 26 17 14 15 24 26 11 25 31 20 24 19 27 19 30
[745] 18 16 24 14 23 19 19 24 18 19 18 19 16 21 18 18 14 19 12 20 27 23 20 25 31 17 17 24 20 32 14
[776] 29 19 26 22 21 21 17 9 19 23 23 19 28 15 19 17 19 26 20 23 19 18 20 14 21 14 22 16 16 12 25
[807] 23 14 13 18 19 22 16 21 25 21 24 13 20 21 24 20 21 35 15 23 16 12 25 16 16 18 28 18 27 19 18
[838] 19 27 25 23 16 26 16 17 17 21 12 20 26 18 22 15 26 16 21 20 16 13 25 14 16 13 23 19 12 23 21
[869] 17 16 17 29 24 16 15 14 17 24 25 22 23 23 24 22 22 26 20 21 18 26 8 20 18 18 22 21 23 23 19
[900] 16 13 23 14 17 20 23 18 20 19 23 22 21 19 19 17 15 22 26 22 17 18 29 14 16 26 21 19 17 15 21
[931] 26 19 23 23 18 23 15 15 24 22 25 16 18 19 13 18 25 19 22 15 18 20 28 15 24 20 17 21 20 23 17
[962] 22 18 25 19 21 21 22 21 18 18 21 17 26 16 23 25 27 33 30 20 22 24 17 14 21 21 24 20 24 23 14
[993] 20 29 12 25 18 6 14 22

> table(rpois(n=1000, lambda = 20))

7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
1 2 3 6 13 17 33 31 45 74 76 77 87 95 86 73 65 59 37 36 28 16 14 12 4 8 2

> plot(table(rpois(n=1000, lambda = 20)))

위 그래프를 보면 λ = 20 이므로 평균이 20인 위치에서 가장 높게 모여있고 , 오른쪽으로 꼬리가 긴 포아송 분포를 따르고 있음을 알 수 있따.

출처: http://rfriend.tistory.com/101 [R, Python 분석과 프로그래밍 (by R Friend)]

'학부공부 > 데이터마이닝과통계' 카테고리의 다른 글

R패키지의 데이터셋을 다뤄보기 ( with mtcars ) (0)	2018.11.30
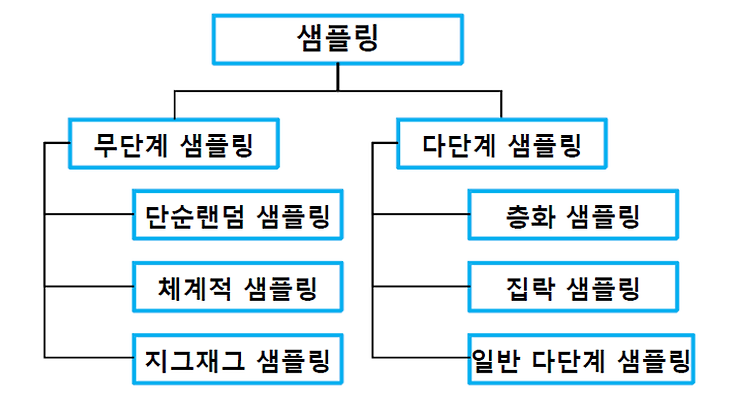
통계학의 개념 (0)	2018.11.27
구글서칭결과크롤링+CSV파일저장시키기 (3)	2018.11.19
Corpus --> VCorpus (2)	2018.11.18
논문제목+논문저자+논문발간일 크롤링 / wordcloud2 (5)	2018.11.18

@IT grow. :: IT grow.

#IT #먹방 #전자기기 #일상

#개발 #일상

'학부공부 > 데이터마이닝과통계' 카테고리의 다른 글

티스토리툴바