[Stanford University CS231n, Spring 2017] Lecture 3 | Loss Functions and Optimization

오늘은 cs231n 3강을 제 소신껏 정리를 해보겠습니다.

저번 시간에는 이미지 분류에 대해서 알아 보았습니다.

조명과 변형 은닉 등의 문제 때문에 

이미지분류가 힘들고 쉽지 않은 일인지 알아 보았습니다

 

 

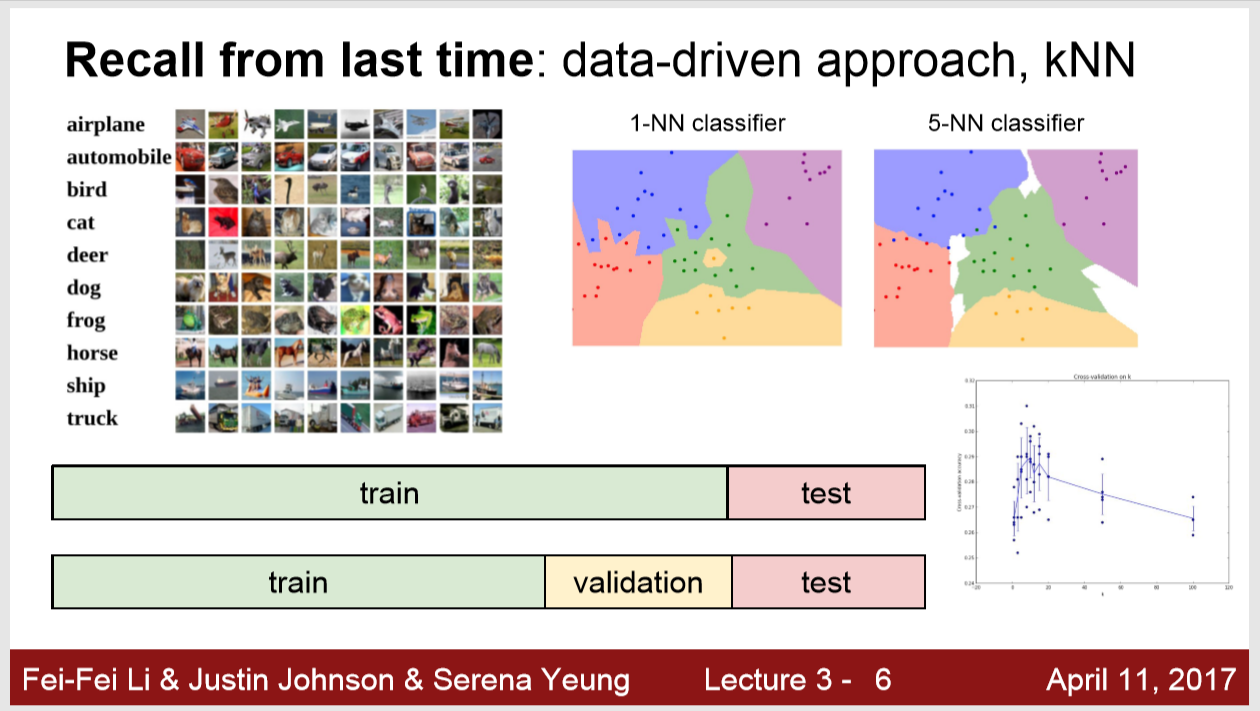
CIFAR-10 데이터셋에 대해서도 알아보았고 , KNN에 대해서도 알아보았습니다.

또한 data-driven방식을 알아보았었는데 

데이터를 훈련시킬 때는 train,test이 2개로만 나누면 좋지 않았다고 배웠습니다.

train,validation,test 3개로 나눠서 test셋은 마지막에 평가할 때 딱 1번만 사용된다고 배웠습니다.

 

 

Linear Classifier에 대해서도 배웠었는데요.

x는 이미지, w는 가중치(weight)를 줘서 score를 뽑아냈었습니다.

 

score에 따라 이미지 분류기에 들어온 이미지를 인식한다고 배웠으며

하나의 분류기를 사용하면 이미지 분류가 잘 안된다는 것 또한 배웠습니다.

 

예를 들면 위 사진의 아랫부분에 해당하는 말머리가 2개처럼 보이는 듯한 문제가 발생하였습니다. 

 

 

저희는 앞서 linear classifier를 배웠었는데요. 여기서 w값을 준다는 것을 배웠습니다.

위 사진을 보겠습니다.

 

위 사진을 통해서 w가 좋은영향을 미치는 지 알아 보아야 할 것입니다.

 

cat의 경우 2.9점을 나타냈고 , 자동차에 대해서는 6.04를 나타냈으며 개구리에 대해서는 

-4.34를 나타냈네요.

 

이를 통해서 cat은 잘 못맞춘 상태이지만 자동차의 경우에는 나름 잘 맞췄다고 생각이 들고 

개구리 같은 경우에는 -의 값이니까 정말 못맞춘 상태라고 생각이 들게 됩니다.

결론적으로는 score는 매우 안좋게 나왔다는 것이며 영향을 주는 w는 매우 안좋다고 말할 수 있게 됩니다.

 

결국에는 이 w가 좋다 혹은 안좋다 라고 판단할 수 있는 방법이 필요합니다.

 

이것이 바로 " loss function " 입니다. 

 

이 loss function은 이 w가 얼마만큼 안좋아~~ 라고 말해주는 것입니다.

 

안 좋은쪽으로 찾는 것이 loss function 이라면 

좋은쪽으로 찾는 것이 optimization 이라고 합니다.

 

 

위 사진을 보겠습니다.

 

고양이,자동차,개구리 세 개의 사진이 있습니다.

 

 

위 사진을 보면 x는 이미지이고 y는 카테고리(라벨)입니다.

라벨값이란 고양이는 0 자동차는 1 개구리는 2 와 같이 숫자로 이미지 당 고유값을 갖는것을 의미합니다.

 

수식 밑에 내려가다 보면 

 

일반적으로 Loss를 구하는 방법이 나와있습니다.

이런 것들이 있구나 하고 넘어가면 될 것 같습니다.

 

각 i 카테고리별 loss를 각각 구합니다.

그런 다음 그걸 싹-다 더합니다.

그리고 나서 카테고리별 개수로 나눠 평균값을 구합니다.

 

이렇게 하면 최종적인 loss값이 됩니다.

이렇게 구한 loss 값을 확인해 보겠습니다.

 

위와 같은 개념으로 위 사진은 서포트 벡터 머신 ( SVM ) loss입니다.

동의어로 hinge loss ( 힌지 로스 ) 라고도 합니다.

 

sj는 정답이 아닌 클래스 score이며 

syi는 정답 클래스 score 입니다.

 

조건을 확인해 보겠습니다.

 

만약 정답 클래스가 정답이 아닌 클래스 + safety margin ( 여기서는 1이라고 표현했네요 ) 값보다 더 크다면 

loss는 0이다 라는 의미입니다.

 

그리고 밑에 조건도 확인해 보겠습니다.

 

만약 위에 조건이 아니라면 ( 정답이 아닌 클래스 - 정답클래스 + safety margin (여기서 1로 표현했네요!) 의 값을 loss로 가진다 라는 의미입니다.

 

간략하게 말하자면 

 

만약에 정답 클래스가 정답이 아닌 클래스보다 safety margin 보다 크면 loss는 0이다 의 뜻입니다.

loss가 0이라는 의미는 매우 안좋다는 의미입니다.

 

 

위 내용을 그래프로 나타낸 것이 위 사진입니다.

더 자세히 알아 보겠습니다.

다음 사진을 보겠습니다.

 

위에서 길게 말한 결론은 파란색 박스라고 생각하시면 됩니다.

 

다음 사진을 보겠습니다.

 

위 사진을 보면 긴 수식과 숫자들이 있는것을 확인할 수 있습니다.

 

위 사진에서는 고양이가 정답 클래스입니다.

 

파란색 박스를 보겠습니다.

보면 자동차 score가 5.1이고 고양이가 3.2입니다.

 

loss가 발생할 것 같다는 생각이 들 것입니다.

 

정답이 아닌 클래스 ( 자동차 5.1 ) - 정답 클래스 ( 고양이 3.2 ) + 1 값을 loss로 줍니다.

 

고양이와 개구리 또한 확인해 보겠습니다.

 

보시다 시피 고양이가 score가 더 높습니다.

 

그렇다면 개구리에 +1을 더해보면 -0.7이 됩니다.

 

그럼에도 고양이 score가 더 높게 나오게 됩니다.

 

그럼 loss가 0이 되는 것입니다.

 

위에서 loss를 구해준 것들을 더 해 보면 2.9 + 0이 되어서 2.9가 됩니다.

 

이 2.9라는 수치는 2.9 만큼 안좋아!! 라는 의미를 갖게 됩니다.

 

위 사진을 보겠습니다.

 

이번에는 자동차를 기준으로 보겠습니다.

 

그런데 자동차 같은 경우에는 자동차가 아닌 클래스에 +1씩 더해주어도 

 

car score에 미치지 못합니다. 

 

이 말은 즉 loss가 다 0이라는 의미가 됩니다.

 

결국엔 loss 최종 값은 0입니다.

 

 

이번에는 개구리를 기준잡아서 보겠습니다.

개구리의 loss값은 12.9가 되는데요.

 

아까 앞에서 본 고양이는 그래도 한개는 맞췄기 때문에 loss가 비교적 낮은 편입니다.

 

그러나 개구리는 분류하는 것에 있어서 12.9만큼 안좋다는 의미이니까 고양이보다 안좋다는 의미를 갖게 됩니다!

 

 

결국에는 최종적으로 2.9 + 0 + 12.9를 하고 클래스가 3개니까 3으로 나눠주게 됩니다.

 

그러면 5.27이라는 최종 loss값이 나오게 됩니다.

 

 

여기서 한 가지 질문을 해보겠습니다.

 

만약 자동차 score의 변동을 주게되면 어떻게 될까?? 라고 말입니다.

 

자동차의 score가 4.9에서 -1이 되어서 3.9가 되었다고 가정을 해봅니다.

 

그래도 loss가 0이 아닙니다.

 

왜냐하면 cat에 +1을 하고 frog에 +1을 하여도 자동차가 더 높기 때문입니다.

 

여기서 SVM hinge loss의 특성을 알 수 있는데요!

 

바로 데이터에 민감하지 않다는 것입니다.

 

이 친구는 score가 몇점인지 관심이 없습니다. 오로지 정답 클래스가 다른 클래스 보다 높니?? 만 관심이 있습니다.

 

 

두번째 질문을 해보겠습니다.

loss의 최소값과 최대값은 어떻게 될까? 입니다.

 

아까 본 hinge loss를 보면 알게 될 것입니다.

 

loss의 최소값은 0이며 , loss의 최대값은 무한대입니다!

 

 

세 번째 질문입니다.

 

만약 w가 매우 작아져서 score가 0에 가까워지면 어떻게 될까? 입니다.

 

계산을 해보면서 확인해 보겠습니다.

 

max ( 0, 0 - 0 + 1 ) + max ( 0, 0 - 0 + 1 ) = 2 

cat , car , frog -->  2 + 2 + 2 / 3 = 2 

loss = C - 1 ( sanity check ) 

 

위 처럼 계산을 해 볼 수 있습니다.

 

그런데 지금은 클래스가 3개 이기 때문에 2 + 2 + 2 / 3 = 2가 되겠습니다.

 

보면 이 값은 클래스 개수 - 1 값이 나오게 됨을 알 수 있습니다.

 

 

 

네 번째 질문입니다.

 

지금까지 저희는 정답 클래스 값은 제외 시키고 구하였습니다

 

왜 제외 시키고 구하였을까요...? 

 

그렇다면 정답 클래스를 포함하여 더하면 어떻게 될까요? 입니다.

 

계산해 보면서 확인해 보겠습니다.

 

 

max ( 0 , 5.1-3.2+1 ) + max ( 0 , -1.7-3.2+1 ) + max ( 0, 3.2-3.2+1 ) 

loss + 1 

최종 loss ( 평균값 ) + 1 

 

계산을 해보면 위 처럼 나오게 됩니다.

 

평균값이 1이 증가하게 되는 것인데요!!

 

지금 우리는 최종 loss가 0이 되길 바라고 있습니다.

 

왜냐하면 loss가 0이여야 가장 좋다고 보기 편한데요 ! 이렇게 하면 1이 가장 좋은 값이 됩니다!

 

이렇게 되면 뭔가 이상하다는 느낌이 올 것입니다.

 

그렇기 때문에 정답 클래스를 빼서 loss가 0이 되도록 하는 것입니다!!

 

 

다섯 번째 질문입니다.

 

만약 합(sum) 대신 평균을 이용하면 어떻게 될까? 입니다.

 

정답부터 말하자면 별 상관 없다는 것입니다.

 

다만 scale만 작아지게 될것입니다. 평균값으로 계산했기 때문입니다.

 

그러나 우리의 주 관심사는 loss 값이기 때문에 scale이 커지던 작아지던 상관이 없습니다.

 

 

여섯 번째 질문입니다.

만약 제곱승을 하게 되면 같을까? 다를까? 입니다.

 

결론부터 말하자면 "다르다" 입니다.

 

일단 제곱을 하면 non linear하게 되고 저렇게 구하는 방법은 squared hinge loss라고 불리우는 방법입니다.

 

추가적으로 얘기해 보자면 상황에 따라 좋게 적용될 때도 있다고 합니다.

 

hinge loss 그래프에서 직선이 아니라 곡선으로 제곱승으로 올라가기 때문입니다.

 

그렇기 때문에 " 매우매우 안좋다 " 혹은 " 매우매우 좋다 " 를 판별할 때 유용하게 사용할 수 있다고 하네요.

 

그러나 일반적으로는 제곱승을 하지 않고 그냥 사용한다고 합니다.

 

 

이 방법을 numpy로 짜면 위처럼 되는데요!

이렇게 되는 구나 하고 그냥 넘어가겠습니다.

 

그런데 말입니다.

 

한가지 문제가 있습니다.

 

우리가 구하는 w가 과연 unique한 값일까요 ??

즉, 유일한 값일까요 ??

 

아니라는 것입니다!!

 

 

위 사진처럼 간단하게 2배,3배 이렇게 배의 값을 취했을 때도 똑같이 0이 나온다는 것입니다.

 

즉 , w는 여러개가 될 수도 있다는 얘기 입니다!!

 

그렇다면 궁금하신 분들이 계실 수 있습니다.

 

w의 값이 여러개가 되도 상관이 없는거 아닌가..? 라고 의문을 갖는 분들이 계실 수 있다는 것입니다.

 

생각을 더 해보겠습니다.

 

train / test 데이터셋이 있다고 가정해 봅시다.

 

이 때 저희는 어떤 부분에 더 관심을 가지게 되나요??

 

바로 test set입니다.

 

새로운 값에 대해서 예측을 하고자 하는데요!!

 

그렇다 보니 test set으로 정확도를 추출하게 되는것 입니다.

 

그런데 지금까지 한 것은 train set에 맞추어 진행이 되었습니다 . 

 

그렇다보니 w가 train set에 맞춰질 것입니다.

 

근데 test set에도 이 w가 맞춰질까요...??

 

정답은 "아닙니다" 입니다.

 

test에서는 해당 w가 안맞을 수 도 있습니다.

 

 

위 사진을 보겠습니다.

 

train에 대해서 위와 같은 모양으로 구했다고 가정해 볼 것입니다.

 

그렇다면 아래 그림과 같은 상황이면 어떻게 될까요?? 

 

 

위 그림에서 초록색 값들을 어떻게 예측하게 될까요!?

 

예측하지 못합니다...

 

이게 과적합 ( 오버피팅 , overfitting ) 이라고 합니다.

 

 

전 그림보다 위 그림처럼 나와있는 초록색 모양이 더 좋을듯 합니다.

 

결론적으로 말하자면 

 

test에도 맞을 수 있는 w값을 찾아야 한다는 것입니다!!

 

그래서 regularization ( 규제 ) 라는 개념이 나오게 됩니다 . 

 

 

왼쪽은 data loss 이고 오른쪽은 regularization 입니다.

data loss는 train 입장에 있고 regularization은 test 입장에 있습니다.

 

가정을 해보겠습니다.

 

train 입장에서 자신한테만 맞는 것을 학습하려고 할 때 regularization은 말을 합니다.

 

"너 그렇게 하면 이정도의 패널티는 감안해야될껄~?! " 

 

라고 말입니다.

 

이렇게 train 과 regularization은 서로 투닥거리면서 최적의 w를 찾아나가게 되는 것입니다.

 

 

위 그림에서 나와있는 것처럼 오컴의 면도날이라는 것은 과학계에서 많이 사용하는 말인데요.

 

간략하게 말하자면 가설을 세우면 단순한게 더 좋다는 것입니다.

 

 

또 많이 사용하는 loss가 있습니다.

 

바로 softmax classifier 입니다 ( 소프트맥스 라고 많이들 부른다고 하네요 ! ) 

 

또한 cross entropy ( 크로스 엔트로피 ) 라고도 불린다고 하네요 !! 

 

위 그림을 보겠습니다.

 

위 그럼처럼 이렇게 있다고 가정해 보겠습니다.

 

 

softmax function은 위와 같습니다.

 

모든 스코어를 exp를 취하고 그걸 다 더한 다음에 원하는 클래스의 점수를 exp 취해서 나눠 줍니다.

 

이렇게 해주면 확률 값이 될 것입니다.

 

예를 들면 1 / 1 + 2 를 하면 1의 확률은 1 / 3이 됩니다 . 

 

 

그리고 나서 내가 원하는 정답 클래스에 -log 를 취해주어서 loss를 구하게 됩니다

 

위 그림처럼 말입니다. 

 

근데 한가지 의문인점이 있을 수도 있습니다. 

 

왜 -log를 취해주는 것이며 exp는 왜 하는 것일까요? 

 

softmax 는 multinomial logistic regression 입니다.

 

로지스틱 회귀는 시그모이드 함수라고도 불리웁니다.

 

exp값이 취해져 있는 형태입니다.

 

그리고 -log를 취하는 이유는 우리가 얼마나 안좋은지를 판단하는 것입니다.

 

x축이 확률이며 , y축이 loss라고 생각하시면 

 

-log를 취할 때 1에 가까워질수록 ( x측 , 우리가 원하는 클래스의 정답률이 1에 가까우면 100% 라는 것이니 좋은것입니다 ) 

 

loss가 0에 가까워집니다 ( y축 ) 

 

그렇기 때문에 -log를 사용하는 것입니다. 

 

예시를 통해서 더 확인해 보겠습니다.

 

 

아까 보았던 예시에서 계산을 해보겠습니다.

 

 

exp를 취하면 위와 같은 값이 나옵니다.

 

 

그리고 전체를 더한 값 ( 188.68 ) 을 각각 나눠줍니다.

 

그러면 24.5는 24.5 / 188.68 이니 0.13 등이 나오게 됩니다

 

이게 확률값이 되고 마지막으로 

 

내가 원하는 정답 클래스에 -log 값을 취해줍니다.

 

즉 이 친구는 0.89만큼 안좋다는 얘기입니다.

 

 

여기서도 질문을 하나 해 볼 수 있습니다.

 

min , max 값은 무엇일까요 ?? 입니다. 

 

최소는 이론적으로 0 입니다. 최대는 이론적으로 무한대 이구요.

 

- log 그래프를 보시면 이해가 되실듯 합니다.

 

 

위에서와 같이 만약 스코어가 0으로 가까워지면 어떻게 될까요??

 

앞서 본 hinge loss에서는 클래스 개수 - 1 ( C - 1 ) 값이었습니다.

 

 

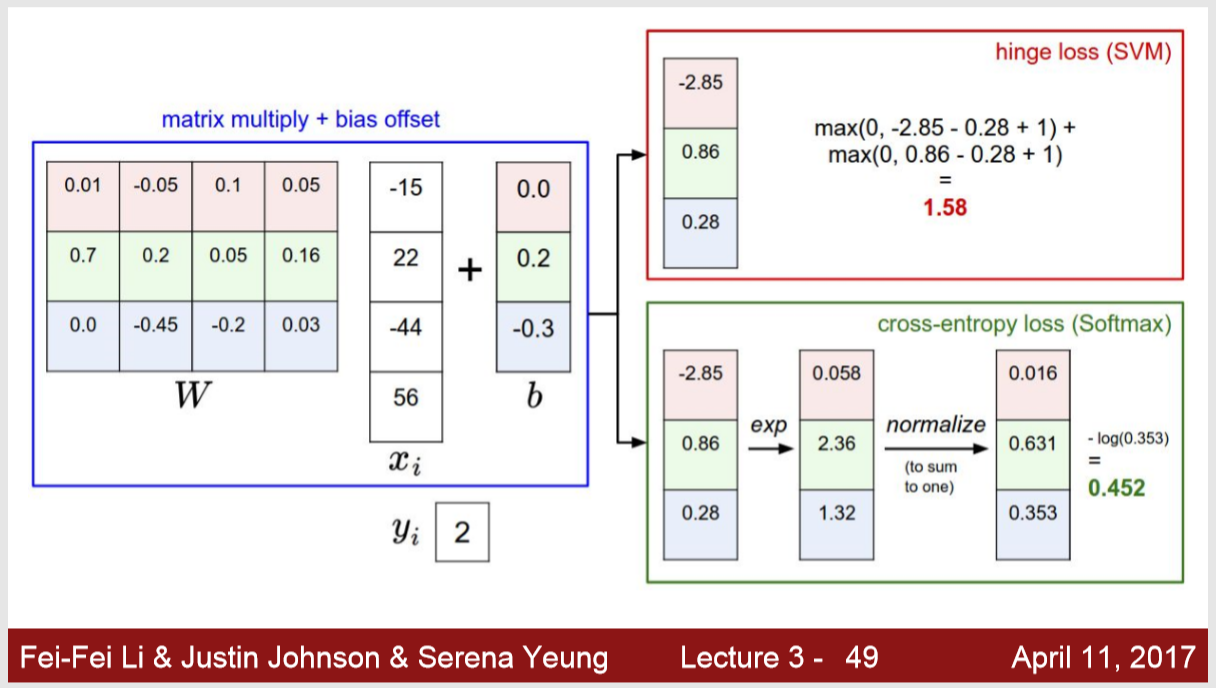
이렇게 score가 나오면 svm hinge loss 와 cross-entropy loss ( softmax ) 의 차이점을 볼 수 있습니다.

 

max 값을 취해서 구하는 것과 exp를 취해서 확률 값으로 만드는 것이냐의 차이를 볼 수 있습니다.

 

 

한가지 더 질문을 할 수 있습니다.

 

만약 datapoint에 변동을 주게 된다면 어떻게 될까? 입니다.

 

앞서 SVM에서 car 점수를 조금 변경시켰을 때 어떻게 됬는지 기억나시나요~!?

 

그냥 hinge loss는 정답 클래스가 정답 클래스가 아닌 클래스 + 1 보다 크면 끝이였습니다.

 

그래서 점수 포인트가 바뀌어도 딱히 영향이 없습니다.

 

앞서 말한 것 처럼 데이터에 둔감한 것입니다.

 

하지만 cross-entropy loss ( softmax function ) 은 다릅니다.

 

이 친구는 확률로 계산되기 때문에 조금만 데이터가 변경되어도 바로 확률에 영향을 미치게 됩니다.

 

반대로 매우 민감한 것입니다!!

 

이것이 둘의 가장 큰 차이점입니다!!

 

요약을 해보자면 위 그림과 같습니다.

 

full loss는 언제나 regularization을 추가한 것입니다!!

 

 

이제 이 w가 안좋아 ! 라는 것을 알게되었습니다.

 

그러면 이제 어떻게 해야할 까요??

 

좋은 값은 어떻게 찾을 수 있는지 알아 보아야 할 것입니다!

 

바로 Optimization 입니다.

 

 

 

그 방법중 하나로써 random search 입니다. 

 

결론부터 말하자면 절대 사용하지 말아야 하는 방법 중 하나입니다.

 

이 방법은 말 그대로 랜덤하게 포인트를 찾는 것입니다.

 

 

그렇다 보니 안좋으면 15.5 %의 정확도가 나올 때도 있고 최고는 95%의 정확도가 나올 때도 있답니다.

 

 

그렇기 때문에 " 경사 하강법 " 을 사용합니다.

 

gradient descent 라고도 불리웁니다.

 

경사를 따라서 조금씩 조금씩 내려가는 것을 상상하시면 될 듯합니다.

 

이렇게 수식으로 하나하나 계산해서 사용하는 방법이 

 

numerical 방법이라고 합니다. 

 

아래 예시를 확인해 보겠습니다 . 

 

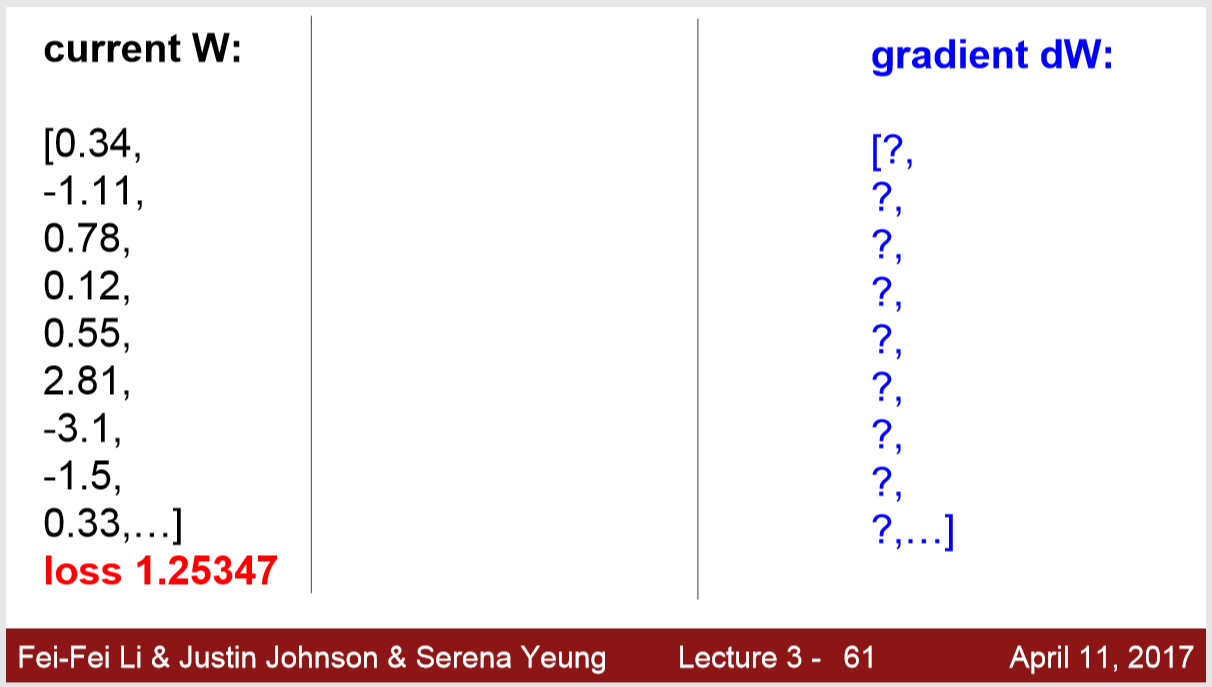
w 와 loss가 위그림처럼 되어 있다고 가정을 해 보겠습니다.

 

 

위 그림 처럼 맨 처음 값을 h를 0에 가깝게 이동시켜 봅니다.

 

loss를 보시면 감소한 것을 확인 하실수 있습니다.

 

 

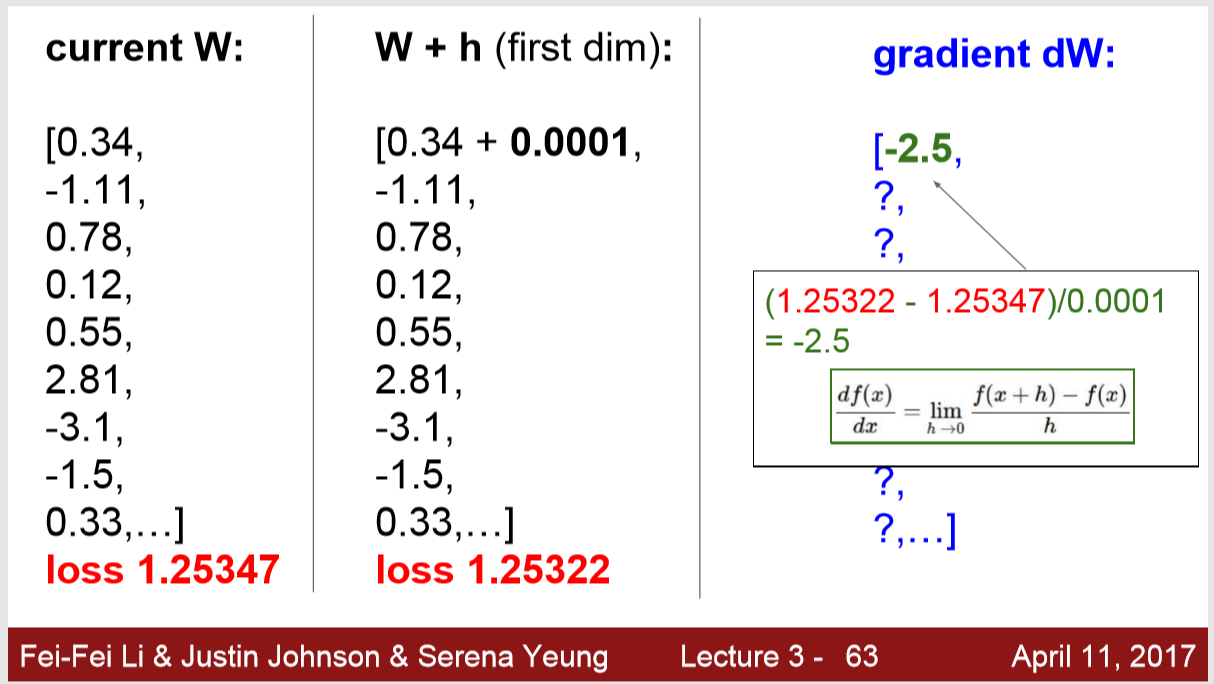
그리고 나서 경사값을 구하면 -2.5가 나왔네요.

 

다음을 보겠습니다.

 

 

얘는 이상하게도 loss가 증가한 것을 확인할 수 있습니다.

 

 

기울기 값은 0.6이 나왔네요!

 

 

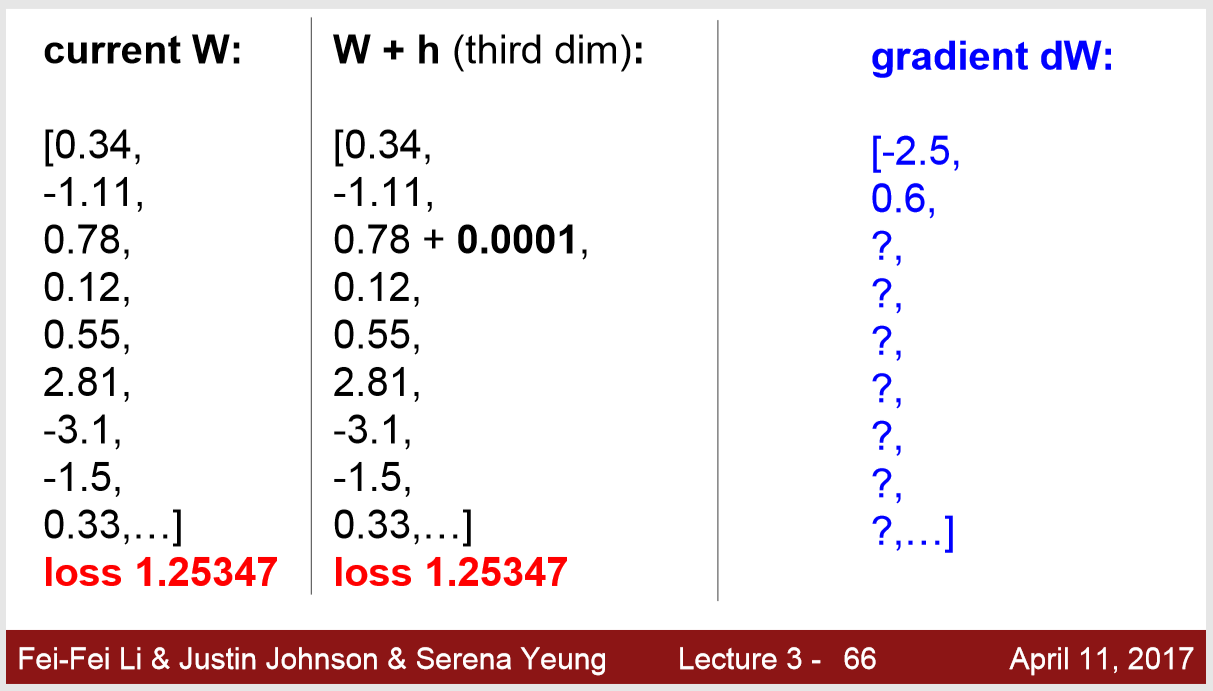
다음값에 또한 h의 값을 더해 줍니다.

 

 

이 친구는 또 이상하게 loss가 감소하지도 않았습니다. 즉 0이 된 것입니다.

 

loss 변화가 없으니까 볼 필요도 없는 것입니다.

 

이처럼 하나하나 수치적 방법으로 계산하는 것이 위 식인데요!

 

하나씩 뜯어보면서 보면 아 ~ 이렇게 하는 구나라고 생각이 들긴 하지만 

 

언제 일일이 하고 있을까 싶습니다.

 

 

우리의 목표는 w가 변화할 때 loss를 알고 싶은 것입니다. 

 

 

그래서 이 2분들이 만들어 놓은 미분식을 이용하면 됩니다. 

 

미분을 사용하여서 analytic gradient ( 해석적 방법 ) 을 사용하면 됩니다!!

 

 

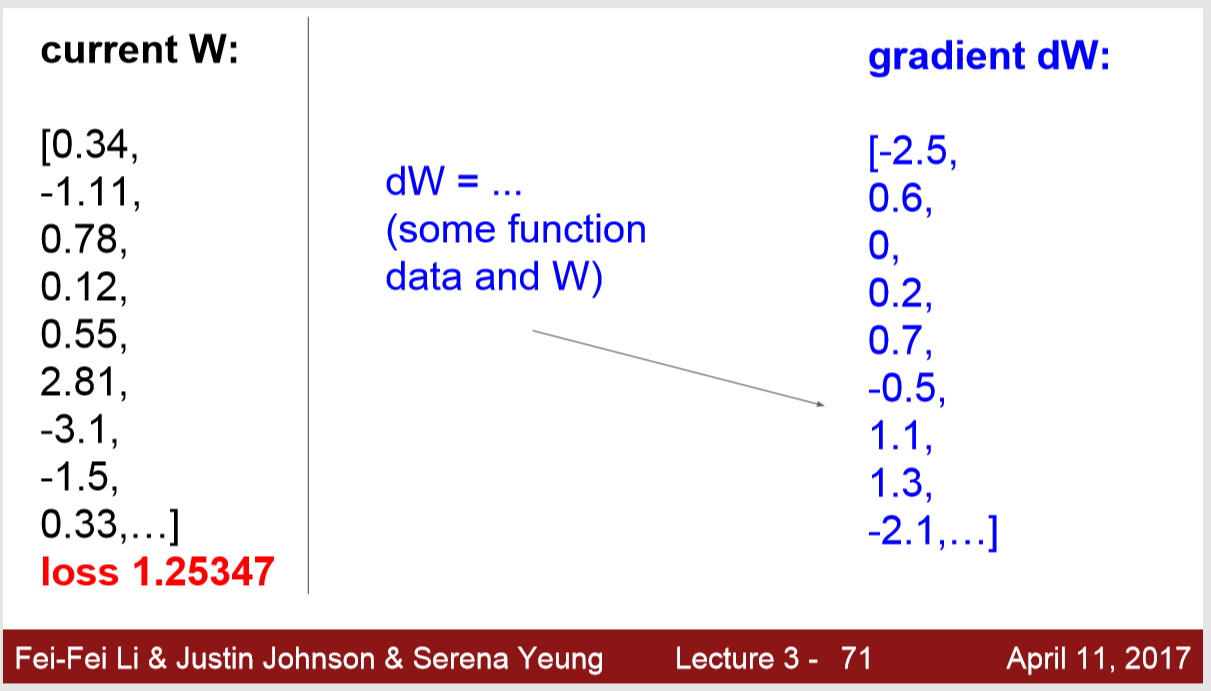
사용하게 되면 위 그림처럼 금방 결과를 추출할 수 있을 것입니다.

 

 

요약을 해보자면 numerical gradient는 정확하지 않으며 느리지만 간편하다는 장점이 있습니다.

 

analytic gradient는 정확하고 빠르지만 에러가 많이 나올 가능성이 있다는 것입니다.

 

보통은 analytic gradient를 사용한다고 합니다 ! 

 

하지만 디버깅 및 점검할 때는 numerical gradient를 사용하기도 합니다!!

 

 

임의의 w 위치에서 가운데 빨간색 지점으로 가는 것이 기울기가 0이 된다는 의미일 테고 저희의 목표이기도 합니다.

 

 

한 가지 더 알아둬야 할 게 있는데 우리는 지금까지 N을 한 번에 올려서 계산을 하였습니다.

 

근데 만약 N이 수천만개 일 수 도 있는데 그럼 매우 비효율적일듯 합니다.

 

왜냐하면 W가 업데이트 되려면 처음부터 끝까지 계산을 하고 업데이트 되는데 

 

수천만개를 계산하고 업데이트하고 또 계산하고 업데이트 하면 매우 느릴 것 입니다

 

그래서 stochastic gradient descent ( SGD ) 를 많이 사용합니다 

 

이 방법은 minibatch를 두어서 데이터 개수를 잘라서 사용하는 것입니다

 

보통 256, 512 처럼 2의 승수로 사용합니다.

 

그래서 256 개를 가지고 w를 업데이트하고 또 다음 256개를 가지고 w를 업데이트 하는 방식으로 진행되는 것입니다.