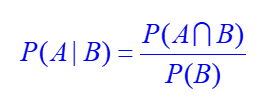

조건부 확률
è 어떤 조건 (B) 이 주어진 상태에서 특정 사건(A)이 발생할 확률
è 모든 원소의 발생확률이 동일하다면
다음과 같이 남학생과 여학생 , 그 남학생과 여학생에 따른 문과출신과 이과출신이 존재한다.
è 한 학생이 문과출신일 때 , 그 학생이 여학생일 조건부 확률
è 한 학생이 여학생일 때 , 그 학생이 문과출신일 조건부 확률
곱의 법칙 (multiplicative law)
è 두 사상 A와B가 동시에 발생할 확률
독립 사상 (independent events)
è 표본공간을 이루고 있는 사건 A와B에 대하여 두 사건 A와 B가 서로 독립이면
다음이 성립하게 된다 .
è 즉 , P(B|A)에서 조건으로 주어진 사건 A가 사건 B에 아무런 영향을 주지 못하므로 , 사건 A와 B는 서로 독립인 관계 성립
è 한 한생이 문과출신일 사상(A)와 , 여학생일 사상(F)의 독립성을 판정해 보자 .
그렇다면 P(A) = 0.40 , P(F) = 0.45 , P(A n F) = 0.25
P(A)P(F) = 0.40 x 0.45 = 0.18 not= P(A n F) = 0.25
위의 공식에 따르면 0.25 와 0.18은 다르기 때문에 , 우리가 예제를 사용한 여학생과 남학생 도표에서는 서로 독립인 관계가 성립 하지 않는다.
베이즈 정리
è 전확률 정리 (theorem of total probability)
표본공간 S를 상호배반인 사상들로 분할 (partition)

Extends
마르코프 결정 과정
è 마르코프 결정 과정(Markov Decision Process)는 의사결정 과정을 모델링하는 수학적인 틀을 제공한다. 이 때 의사결정의 결과는 의사결정자의 결정에도 좌우되지만, 어느 정도 임의적으로 주어진다. 마르코프 결정 과정은 동적 계획법과 강화 학습 등의 방법으로 푸는 넓은 범위의 최적화 문제에 유용한 도구로 활용되며, 로봇 공학, 제어 자동화, 경제학, 제조업 등의 영역에서 폭넓게 사용되고 있다
베이즈 네트워크
è 빌리프 네트워크 or 방향성 비순환 그래픽 모델은 랜덤 변수의 집합과 방향성 비순환 그래프를 통하여 그 집합을 조건부 독립으로 표현하는 확률의 그래픽 모델이다.
è 예를 들어서 베이지안 네트워크는 질환과 증상 사이의 확률 관계를 나타낼 수 있다. 증상이 주어지면 , 네트워크는 다양한 질병의 존재 확률을 계산할 수 있다.
출처 : https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EB%84%A4%ED%8A%B8%EC%9B%8C%ED%81%AC
'학부공부 > 데이터마이닝과통계' 카테고리의 다른 글
| 특정 버스의 버스경로에서 특정 정류장 위치 뽑기. (0) | 2018.12.18 |
|---|---|
| 데이터셋을 활용하여서 회귀분석을 해보자. (0) | 2018.12.03 |
| R패키지의 데이터셋을 다뤄보기 ( with mtcars ) (0) | 2018.11.30 |
| 통계학의 개념 (0) | 2018.11.27 |
| 다양한 확률분포 (0) | 2018.11.24 |

#IT #먹방 #전자기기 #일상
#개발 #일상