
라쏘
선형 회귀에 규제를 적용하는 데 Ridge의 대안으로 Lasso가 있다.
릿지 회귀에서와 같이 라쏘도 계수를 0에 가깝게 만들려고 한다.
하지만 방식이 조금 다르고 , 이를 L1 규제라고 한다.
L1 규제의 결과로 라쏘를 사용할 때 어떤 계수는 정말 0이 된다
이 말은 모델에서 완전히 제외되는 특성이 생긴다는 뜻이다.
어떻게 보면 특성 선택 ( feature selection )이 자동으로 이뤄진다고 볼 수 있다.
일부 계수를 0으로 만들면 모델을 이해하기 쉬워지고 이 모델의 가장 중요한 특성이 무엇인지 드러난다.
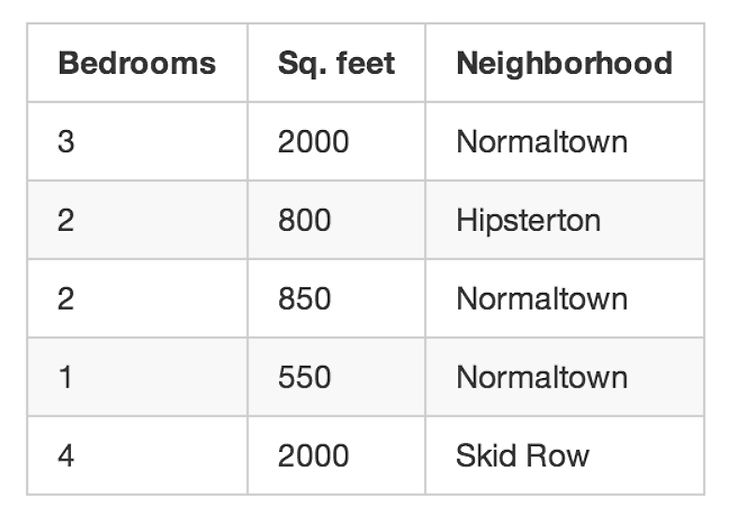
확장된 보스턴 주택가격 데이터셋에 라쏘를 적용해 보겠다.
코드를 통해서 확인해 보자 .
from sklearn.linear_model import Lasso
import mglearn
from sklearn.model_selection import train_test_split
import numpy as np
X,y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lasso = Lasso().fit(X_train, y_train)
필요한 라이브러리와 보스턴 데이터를 가져온 뒤 테스트 , 훈련으로 나누어 준 뒤 Lasso로 fit을 해준다.
print("training set score : {:.2f}".format(lasso.score(X_train, y_train)))
print("test set score : {:.2f}".format(lasso.score(X_test,y_test)))
print("Number of attributes used : {}".format(np.sum(lasso.coef_ !=0)))
Lasso로 어떠한 값이 찍히는지 결과값을 확인해 본다.
training set score : 0.29
test set score : 0.21
Number of attributes used : 4
위 결과에서 볼 수 있듯이 Lasso는 훈련 세트와 테스트 세트 모두에서 결과가 좋지 않다.
이는 과소적합이며 105개의 특성 중 4개만 사용한 것을 볼 수 있다.
Ridge와 마찬가지로 Lasso도 계수를 얼마나 강하게 0으로 보낼지를 조절하는 alpha 매개변수를 지원한다.
위는 기본값인 alpha=1.0을 사용했다.
과소적합을 줄이기 위해서 alpha 값을 줄여보겠다.
이렇게 하려면 max_iter(반복 실행하는 최대 횟수)의 기본값을 늘려야 한다.
"max_iter" 기본값을 증가시키지 않으면 max_iter 값을 늘리라는 경고가 발생한다.
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("training set score_(L0001) : {:.2f}".format(lasso001.score(X_train, y_train)))
print("test set score_(L0001) : {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of attributes used_(L0001) : {}".format(np.sum(lasso001.coef_ !=0)))
결과 값은 다음과 같다 .
training set score_(L0001) : 0.90
test set score_(L0001) : 0.77
Number of attributes used_(L0001) : 33
alpha 값을 낮추면 모델의 복잡도는 증가하여서 ,훈련 세트와 테스트 세트에서의
성능이 좋아진다.
성능은 Ridge보다 조금 좋은데 , 사용된 특성은 105개 중 33개뿐이어서 ,
모델을 분석하기가 조금 더 쉽다 .
그렇지만 , alpha 값을 너무 낮추면 규제의 효과가 없어져 과대적합이 되기때문에
LinearRegression의 결과와 비슷해진다.
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print("training set score_(L00001) : {:.2f}".format(lasso00001.score(X_train, y_train)))
print("test set score_(L00001) : {:.2f}".format(lasso00001.score(X_test, y_test)))
print("Number of attributes used_(L00001) : {}".format(np.sum(lasso00001.coef_ !=0)))
결과 값은 다음과 같다 .
training set score_(L00001) : 0.95
test set score_(L00001) : 0.64
Number of attributes used_(L00001) : 96
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
ridge01 = Ridge(alpha=0.1).fit(X_train,y_train)
plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25,25)
plt.xlabel("Count List")
plt.ylabel("Coefficient size")
plt.show()
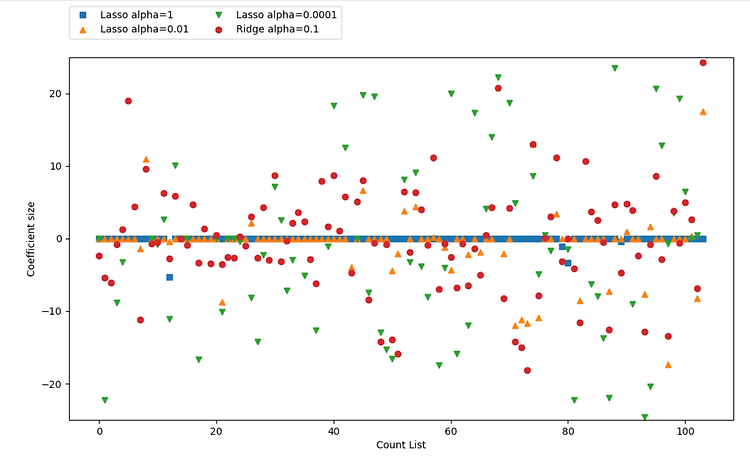
위 코드를 찍어 보면 다음과 같다 .

alpha=1 일때 계수 대부분이 0일 뿐만 아니라 나머지 계수들도 크기가 작다는 것을
알수 있다.
alpha를 0.01로 줄이면 대부분의 특성이 0이 되는 분포를 얻게 된다.
alpha=0.0001이 되면 계수 대부분이 0이 아니고 값도 커져 규제받지 않은 모델을 얻게된다.
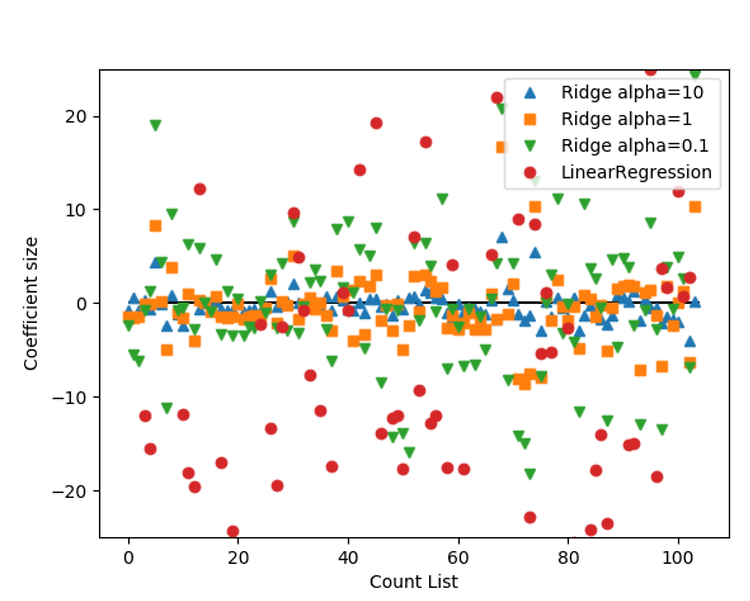
비교를 위해서 릿지 회귀를 원 모양으로 나타냈다.
alpha=0.1 인 Ridge 모델은 alpha=0.01인 라쏘 모델과 성능이 비슷하지만
Ridge를 사용하면 어떤 계수도 0이 되지 않는다 .
실제로 이 두 모델중 보통은 릿지 회귀를 선호한다.
하지만 특성이 많고 그 중 일부분만 중요하다면 Lasso가 더 좋은 선택일 수 있다.
또한 분석하기 쉬운 모델을 원한다면 Lasso가 입력 특성 중 일부만 사용하므로
쉽게 해석할 수 있는 모델을 만들어 줄 것이다.
scikit-learn은 Lasso와 Ridge의 페널티를 결합한 ElasticNet도 제공한다 .
실제로 이 조합은 최상의 성능을 내지만 , L1규제와 L2 규제를 위한 매개변수 두 개를 조정해야 한다.
'학부공부 > 빅데이터기술' 카테고리의 다른 글
| 나이브 베이즈 분류기 ( Naive Bayes Classifier ) (0) | 2019.04.09 |
|---|---|
| 가중치 ( weight ) (0) | 2019.04.09 |
| 릿지 ( Lidge ) (0) | 2019.04.08 |
| 최소제곱법 ( ordinary least squares ) - based on Extended_Boston datasets (0) | 2019.04.07 |
| 최소제곱법 ( ordinary least squares ) - based on wavedatasets (0) | 2019.04.07 |

#IT #먹방 #전자기기 #일상
#개발 #일상