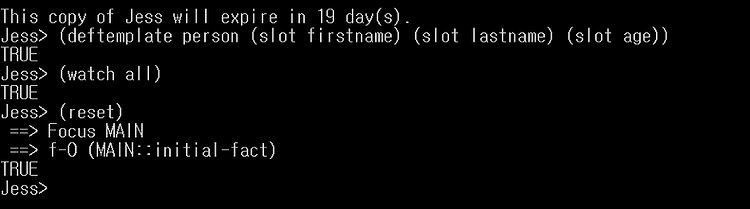
오늘은 저번과 동일하게 Jess 기초 실습을 해 볼 것이다. 코드를 통해서 Jess는 어떻게 쓰는지 알아 본다. firstname, lastname , age를 속성으로 갖는 person ( template )를 만들어 본다 .watch all 로써 , 확인을 해본다.reset함으로써 최종 완료를 한다. 하나의 규칙을 만들어 본다.세 개의 값을 갖는 grocery-list 변수이다 .만약 이 변수가 3개의 값을 갖는다면 , printout 문이 실행이 될 것이다. 바로 확인해 본다 .assert 로써 grocery-list 에 각각의 값을 대입해 본다.(run)으로 실행하게 되면 , 규칙에 걸려서 , 규칙의 printout이 출력된다. 또하나의 규칙을 새워보자.위의 규칙은 위에서 만들어 놓은 grocer..

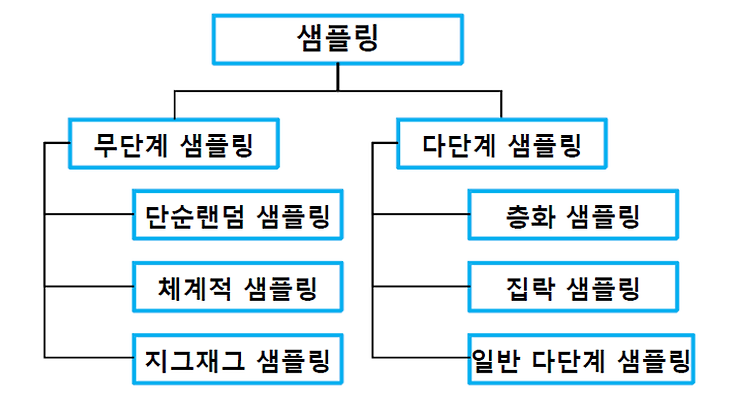
통계학이란? 1. 불확실한 상황 하에서 데이터에 근거하여 과학적인 의사결정을 하기 위한 이론과 방법의 체계 통계학의 활용분야 1. 데이터의 수집 , 분류 , 표현 , 분석 , 추론 , 해석 2. 통계학자의 역할 è 필요한 데이터의 형태 è 데이터를 수집하는 방법 è 문제에 대한 최선의 답을 구하기 위한 분석방법 통계학의 연구분야 1. 통계적 이론과 방법론 개발 2. 통계적 방법론 응용 모집단과 표본 1. 모집단 ( population ) è 통계분석의 연구대상이 되는 모든 개체들의 집합 , 올바른 의사결정을 하기 위해 관심을 갖고 연구해야 할 대상 Ex ) 총학 선거 2명 = 모집단 2. 모수 ( parameter ) è 모집단의 특성을 나타내는 수치이며 , 올바른 의사결정을 위해 특별히 관심을 갖는 모..

저번에 이어서 Jess는 어떻게 사용하는지에 대해서 알아 보겠다. def = 정의하다 라는 의미 persion_template를 하나 만들어 주고 , slot 으로 firstname , lastname , age를 할당해 준다. watch all 로 확인을 해본다.(reset)으로 확인해 보면 assert 해준것이 없이 때문에 initial - fact 만 존재하는것을 확인할 수 있다. 다음은 rule에 대해서 알아보겠다하나의 규칙을 설정해 주는 것이다. 사용법은 다음과 같다.defrule로써 하나의 toddlers의 규칙을 만들어 주게 되는데, 들어오는 매개변수 person의 age가 3보다 작게된다면 printout 이 실행이 될 것이다. 만들어 주고 나서 , assert 로써 person 의 age..

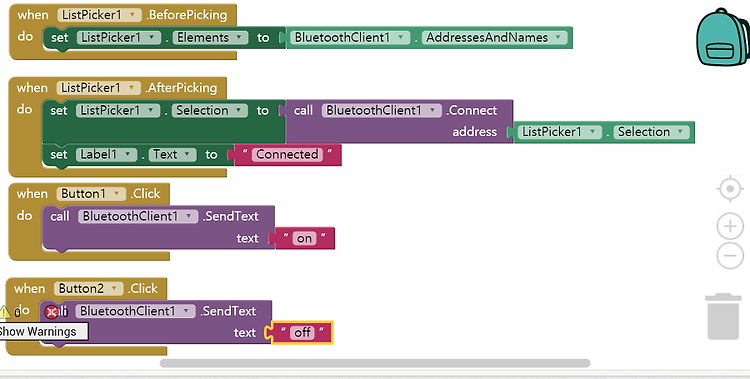
저번에 MIT - app - inventor2에 대해서 간략하게 설명해 보는 시간을 가졌었다. 나는 app - inventor를 쓰고자 하는 목표가 있다.app-inventor을 사용해서 arduino의 전원 on / off를 목표로 하고 있는데, app - inventor를 사용해서 , arduino의 블루투스 on / off 를 해보겠다. 먼저 디자인은 다음과 같이 간략하게 해주어 보았다. 다음은 Blocks 이다 .먼저 초기 작업은 , BluetoothClient1 로써 주소 이름들을 가져온다.Picking 이란게 어떤 신호를 잡았을 때 라고 이해하면 될 것 같다.신호를 잡았을 경우에 아까 연결한 블루투스의 주소에 연결을 하고 , Lable1인 Text에 Connected 텍스트를 띄어준다. 그리고..

오늘은 아두이노 프로젝트를 진행 하던 중에 , MIT 앱 인벤터를 사용해서 개발 환경을 구축해야 하는 상황이 생겼다. 그래서 이게 무엇인지 , 어떻게 사용하는 것인지 정리해 보겠다 1. MIT 앱 인벤터 개발 환경에 대해 이해한다.è 크롬 웹브라우저 설치è 앱 인벤터 홈페이지 접속 à 로그인 ( 구글계정 ) 구글에 또는 특정 검색창에 MIT-app-inventor2를 들어가면 된다. 프로젝트는 만들었다는 가정하에 설명해 보겠다 Block 클릭하면 다음과 같은 화면이 보일 것이다 이 개발 환경은 블록 코딩을 기반으로 한다. Blocks 내에 있는 Built-in은 공통 블록이며 , 항상 사용가능하다 내장 블록은 계산이나 논리연산 텍스트 연산이나 제어를 수행한다. 바로 밑에 있는 부분은 컴포넌트 블록이다 사..

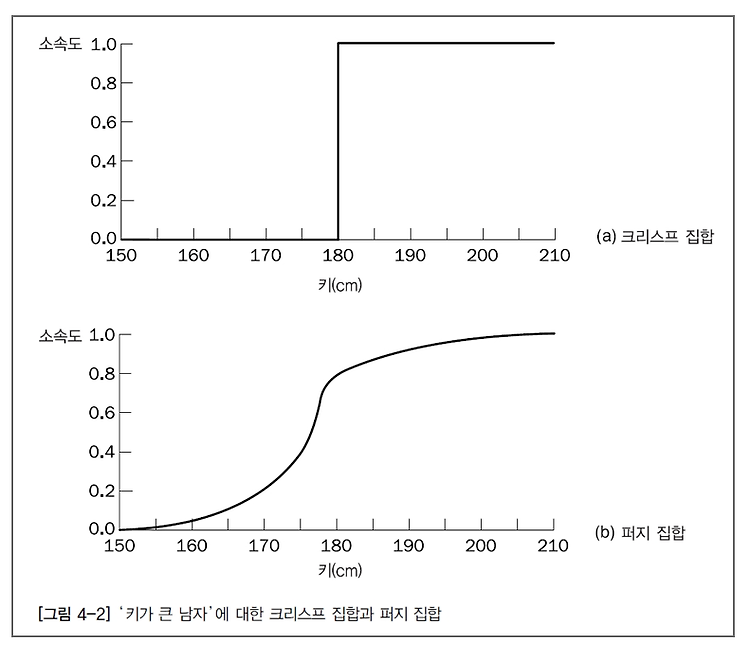
퍼지전문가시스템 퍼지 논리 : 모호한 대상을 다루는 논리 , 퍼지 집합 , 모호한 정도를 조절할 수 있는 집합에 대한 이론 , 퍼지 용어를 표현하고 조작하기 위한 새로운 논리 불 논리 ( Boolean Logic ) : 전통적인 논리는 참과 거짓이 확실하게 구분된다 . 퍼지의 장점 1. 퍼지라는 용어는 구체적이고 직접적이며 , 설명적이어서 무엇을 의미하는지 쉽게 이해할 수 있음 왜 논리일까?? 1. 모호성은 퍼지 집합론에 항상 존재하고 , 퍼지 논리는 이 이론의 일부분일 뿐이다. 그러나 자데는 퍼지 논리라는 용어를 좀 더 넓은 뜻으로 사용했음 2. 2차 논리인 불 논리와 달리 퍼지 논리는 다치 논리이다 . 퍼지 논리는 소속도와 진리도를 다룬다. 3. 퍼지 논리는 0(완전한 거짓) 과 1(완전한 참) 사이..